
【题目】设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数f(x)的单调性.
【答案】
(1)
【解答】
解:由题意:![]() 即
即 ![]() 解得
解得![]()
(2)
【解答】
解:f'(x)=3x2-6x+9=3(x2-2x+3)=3(x-3)(x+1)
当 x<-1 或 x>3 时, f'(x)>0 , 所以f(x) 的单调递增区间为![]() 与
与![]()
当 -1<x<3 时, f'(x)<0 , 所以f(x) 的单调递减区间为 (-1,3)
【解析】本题主要考查了利用导数研究函数的单调性,解决问题的关键是根据导数的几何意义及利用导数求函数的单调区间,属基础题
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数(0,
有如下性质:如果常数t>0,那么该函数(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)= ![]() ,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
(2)对于(1)中的函数f(x)和函数g(x),若对于任意的x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2,8),B(x1 , y1),C(x2 , y2)在抛物线 ![]() 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.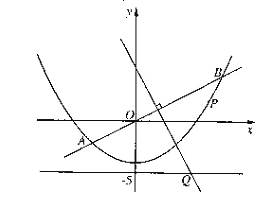
(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方(含A、B)的动点时,求ΔOPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
已知直线l:ρsin(θ+![]() )=
)=![]() m,曲线C:
m,曲线C: 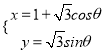
(1)当m=3时,判断直线l与曲线C的位置关系;
(2)若曲线C上存在到直线l的距离等于![]() 的点,求实数m的范围.
的点,求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( ) 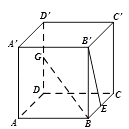
A.120°
B.90°
C.60°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com