
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
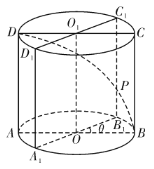
(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知甲箱中装有3个红球,2个黑球,乙箱中装有2个红球,3个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,规定顾客购物1000元以上,可以参与抽奖一次,设奖规则如下:每次分别从以上两个箱子中各随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,奖金300元;摸出的球中有3个红球,则获得二等奖,奖金200元;摸出的球中有2个红球,则获得三等奖,奖金100元;其他情况不获奖,每次摸球结束后将球放回原箱中.
(1)求在1次摸奖中,获得二等奖的概率;
(2)若3人各参与摸奖1次,求获奖人数X的数学期望![]() ;
;
(3)若商场同时还举行打9折促销活动,顾客只能在两项促销活动中任选一项参与.假若你购买了价值1200元的商品,那么你选择参与哪一项活动对你有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠APC=90°,∠BPD=120°,PB=PD.
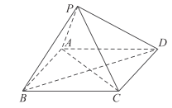
(1)求证:平面APC⊥平面BPD;
(2)若AB=2AP=2,求三棱锥C-PBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 以
以![]() 为圆心,4为半径;又直线
为圆心,4为半径;又直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(Ⅰ)求直线![]() 和圆
和圆![]() 的普通方程;
的普通方程;
(Ⅱ)试判定直线![]() 和圆
和圆![]() 的位置关系.若相交,则求直线
的位置关系.若相交,则求直线![]() 被圆
被圆![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下五个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() ;
;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
![]() 函数
函数![]() 的最小值4;
的最小值4;
则上述结论中正确的是______(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上的动点P(![]() )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为![]()
(1)求曲线C的方程。
(2)过点M(1,2)的直线![]() 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(100,100),则下列选项正确的是( )
(参考数值:随机变量ξ服从正态分布![]() ,则P(μ﹣σ<ξ<μ+σ)=0.6826),P(μ﹣2σ<ξ<μ+2σ)=0.9544,P(μ﹣3σ<ξ<μ+3σ)=0.9974)
,则P(μ﹣σ<ξ<μ+σ)=0.6826),P(μ﹣2σ<ξ<μ+2σ)=0.9544,P(μ﹣3σ<ξ<μ+3σ)=0.9974)
A.E(X)=100B.D(X)=100
C.P(X≥90)=0.8413D.P(X≤120)=0.9987
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com