
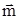 =
=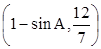 ,
,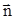 =(cos2A,2sinA),且
=(cos2A,2sinA),且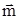 ∥
∥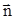 .
.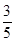 ;(2) 当cosA=
;(2) 当cosA=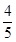 时, a=
时, a= ;当cosA=-
;当cosA=-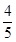 时, a=3
时, a=3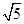 。
。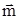 ∥
∥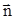 ,∴
,∴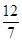 cos2A=(1-sinA)·2sinA, 3分
cos2A=(1-sinA)·2sinA, 3分 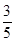 或sinA=-2(舍去). 6分
或sinA=-2(舍去). 6分 bcsinA=3,b=2,sinA=
bcsinA=3,b=2,sinA=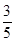 ,得c=5, 8分
,得c=5, 8分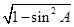 =±
=±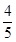 ,
,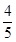 时,a2=13⇒a=
时,a2=13⇒a= ;
;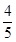 时,a2=45⇒a=3
时,a2=45⇒a=3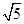 . 13分
. 13分

科目:高中数学 来源:不详 题型:单选题
 与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30
与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30 ,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为
,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com