
分析 依照偶函数的定义,对定义域内的任意实数,f(-x)=f(x),且定义域关于原点对称,a-1=-2a,求出a,b,即可得出结论.
解答 解:∵f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,
∴f(-x)=f(x),∴b=0,
又 a-1=-2a,
∴a=$\frac{1}{3}$,
∴a+b=$\frac{1}{3}$,
f(a)=f($\frac{1}{3}$)=$\frac{1}{3}×(\frac{1}{3})^{2}$=$\frac{1}{27}$.
故答案为:$\frac{1}{3}$,$\frac{1}{27}$.
点评 本题考查偶函数的定义,对定义域内的任意实数,f(-x)=f(x);奇函数和偶函数的定义域必然关于原点对称,定义域区间2个端点互为相反数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a<-3 | B. | $-\frac{3}{2}<a<-\frac{3}{4}$ | C. | $-3<a<-\frac{3}{4}$ | D. | $-\frac{3}{2}<a<-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
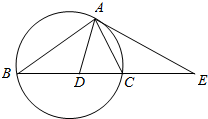 如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:
如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC相交于点D,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com