
| A.168 | B.96 | C.72 | D.144 |


科目:高中数学 来源:不详 题型:单选题
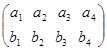 满足下列条件:①每行中的四个数所构成的集合均为
满足下列条件:①每行中的四个数所构成的集合均为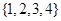 ;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
;②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )| A.48 | B.72 | C.168 | D.312 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
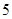 个程序,其中程序
个程序,其中程序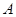 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序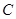 和
和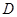 实施时必须相邻,则实验顺序的编排方法共有( )
实施时必须相邻,则实验顺序的编排方法共有( )| A.15种 | B.18种 | C.44种 | D.24种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.6种 | B.12种 | C.24种 | D.48种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com