
【题目】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,直线
,直线![]() 与平面
与平面![]() 成
成![]() 角,
角, ![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() .
.

(Ⅰ)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.
【答案】(Ⅰ)证明见解析;(Ⅱ) 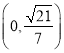 .
.
【解析】试题分析:由题意可得直线![]() 与平面
与平面![]() 所成角是
所成角是![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,由余弦定理得
,由余弦定理得![]() 或
或![]() .
.
(Ⅰ)若![]() ,则
,则![]() ,由勾股定理可得
,由勾股定理可得![]() ,又
,又![]() ,据此可得
,据此可得![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,则
,则![]() ,故
,故![]() ,
, ![]() ,
,
设![]() 是
是![]() 到面
到面![]() 的距离,
的距离, ![]() 是
是![]() 到面
到面![]() 的距离,则
的距离,则![]() ,
,
由等体积法可得![]() ,
, ![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]()
![]() ,据此可得直线
,据此可得直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围为
所成角的正弦值的取值范围为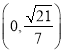 .
.
试题解析:
∵![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角是
所成角是![]() ,
, ![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,由余弦定理得
,由余弦定理得![]() 或
或![]() .
.
(Ⅰ)若![]() ,则
,则![]() ,∴在
,∴在![]() 中
中![]() .∴
.∴![]() ,
,
又![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,
,
设![]() 是
是![]() 到面
到面![]() 的距离,
的距离, ![]() 是
是![]() 到面
到面![]() 的距离,则
的距离,则![]() ,
,
由等体积法: ![]() ,
,
∴![]() ,∴
,∴![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
![]()
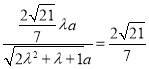
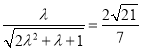
![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]()
故直线![]() 与平面
与平面![]() 所成角的正弦值的取值范围为
所成角的正弦值的取值范围为 .
.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果执行右边的程序框图,输入正整数N(N≥2)和实数a1 , a2 , …,an , 输出A,B,则( ) 
A.A+B为a1 , a2 , …,an的和
B.![]() 为a1 , a2 , …,an的算术平均数
为a1 , a2 , …,an的算术平均数
C.A和B分别是a1 , a2 , …,an中最大的数和最小的数
D.A和B分别是a1 , a2 , …,an中最小的数和最大的数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市某年11月1日—20日监测最高最低温度及差值数据如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高温度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低温度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的频率分布表及频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;

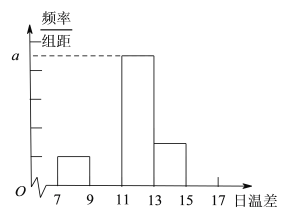
(Ⅱ)从日温差大于等于![]() 的这些天中,随机选取2天.求这两天中至少有一天的温差在区间
的这些天中,随机选取2天.求这两天中至少有一天的温差在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x∈(0, ![]() ),则函数f(x)=sinxtanx+cosxcotx的值域为( )
),则函数f(x)=sinxtanx+cosxcotx的值域为( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在去年的足球甲![]() 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com