
【题目】在正方体![]() 中,
中, ![]() 在线段
在线段![]() 上运动且不与
上运动且不与![]() ,
, ![]() 重合,给出下列结论:
重合,给出下列结论:
①![]() ;
;
②![]() 平面
平面![]() ;
;
③二面角![]() 的大小随
的大小随![]() 点的运动而变化;
点的运动而变化;
④三棱锥![]() 在平面
在平面![]() 上的投影的面积与在平面
上的投影的面积与在平面![]() 上的投影的面积之比随
上的投影的面积之比随![]() 点的运动而变化;
点的运动而变化;
其中正确的是( )
A. ①③④ B. ①③
C. ①②④ D. ①②
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知cosA= ![]() ,b=5c.
,b=5c.
(1)求sinC;
(2)若△ABC的面积S= ![]() sinBsinC,求a的值.
sinBsinC,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
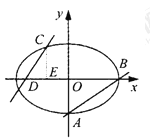
(1)求椭圆的方程.
(2)已知定点![]() ,若直线
,若直线![]() 与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某赛季甲、乙两名篮球运动员参加的每场比赛得分的茎叶图,由甲、乙两人这几场比赛得分的中位数之和是( ) 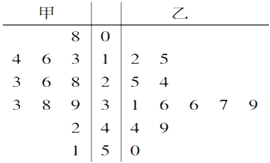
A.65
B.64
C.63
D.62
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据
房屋面积(平方米) | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出散点图
(2)求线性回归方程
(3)根据(2)的结果估计房屋面积为150平方米时的销售价格.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为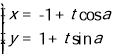 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com