
给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
①在 中,若
中,若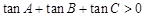 ,则
,则 是锐角三角形;
是锐角三角形;
②在 中,
中, 是
是 的充要条件;
的充要条件;
③已知非零向量 ,则“
,则“ ”是“
”是“ 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;
④命题“在三棱锥 中,已知
中,已知 ,若点
,若点 在
在 所在的平面内,则
所在的平面内,则 ”的否命题为真命题;
”的否命题为真命题;
⑤函数 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数,那么
为恒均变函数,那么 为恒均变函数
为恒均变函数
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:022
给出下列命题:①正角的三角函数值是正的,负角的三角函数值是负的;②设P(x,y)是角a终边上的一点,因为![]() ,所以a的正弦值与点P的纵坐标y成正比;③若sinq ×cosq>0,则q一定在第一象限;④两个角的差是2p的整数倍,则这两个角的同一个三角函数的值必相等;⑤若角a的终边在y轴上,则角a的正弦线是单位长度的有向线段,其中正确命题的序号是________。(将正确的都写出来)
,所以a的正弦值与点P的纵坐标y成正比;③若sinq ×cosq>0,则q一定在第一象限;④两个角的差是2p的整数倍,则这两个角的同一个三角函数的值必相等;⑤若角a的终边在y轴上,则角a的正弦线是单位长度的有向线段,其中正确命题的序号是________。(将正确的都写出来)
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出下列命题:
①正四棱柱是正多面体;
②正四棱柱是简单多面体;
③简单多面体是凸多面体;
④以正四面体各面的中心为顶点的四面体仍然是正四面体;
其中正确的命题个数为
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)动点A′在平面ABC上的射影是线段AF
(2)三棱锥A′—FED的体积有最大值;
(3)恒有平面A′GF⊥平面BCED;
(4)异面直线A′E与BD不可能互相垂直;
(5)异面直线FE与A′D所成角的取值范围是(0,![]() ].
].
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第82课时):第九章 直线、平面、简单几何体-球与多面体(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com