
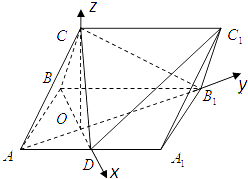
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
【答案】
(1)证明:由题意,因为ABB1A1是矩形,
D为AA1中点,AB=1,AA1= ![]() ,AD=
,AD= ![]() ,
,
所以在直角三角形ABB1中,tan∠AB1B= ![]() ,
,
在直角三角形ABD中,tan∠ABD= ![]() ,
,
所以∠AB1B=∠ABD,
又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,
即BD⊥AB1,
又因为CO⊥侧面ABB1A1,AB1侧面ABB1A1,
所以CO⊥AB1
所以,AB1⊥面BCD,
因为BC面BCD,
所以BC⊥AB1.
(2)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,﹣ ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0,0),C(0,0,
,0,0),C(0,0, ![]() ),B1(0,
),B1(0, ![]() ,0),D(
,0),D( ![]() ,0,0),
,0,0),
又因为 ![]() =2
=2 ![]() ,所以
,所以 ![]()
所以 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ),
),
设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则根据 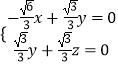 可得
可得 ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() )是平面ABC的一个法向量,
)是平面ABC的一个法向量,
设直线C1D与平面ABC所成角为α,则sinα= 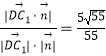 .
.
【解析】(1)要证明BC⊥AB1 , 可证明AB1垂直于BC所在的平面BCD,已知CO垂直于侧面ABB1A1 , 所以CO垂直于AB1 , 只要在矩形ABB1A1内证明BD垂直于AB1即可,可利用角的关系加以证明;(2)分别以OD,OB1 , OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求出 ![]() ,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.
,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.
【考点精析】掌握空间角的异面直线所成的角和用空间向量求直线与平面的夹角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则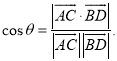 ;设直线
;设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: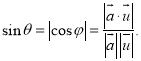 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:
(1)当|OA|十|OB|取得最小值时,直线l的方程;
(2)当|MA|2+|MB|2取得最小值时,直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q. 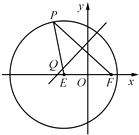
(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Γ相交于A,B两点,直线AO,l,OB的斜率分别为k1 , k,k2(其中k>0),若k1 , k,k2恰好构成公比不为1的等比数列,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α﹣y轴﹣β的大小等于30°.已知β内的曲线C′的方程是3(x﹣2 ![]() )2+4y2﹣36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是 .
)2+4y2﹣36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失. 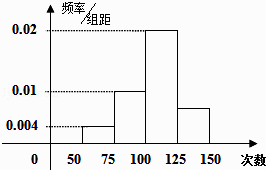
(Ⅰ) 已知第1小组频数为10,求参加这次测试的人数?
(Ⅱ) 求第4小组在y轴上的对应值;
(Ⅲ) 若次数在75次以上 ( 含75次 ) 为达标,试估计该年级跳绳测试达标率是多少?
(Ⅳ) 试估计这些数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1+a2+…+an+2n= ![]() (an+1+1),n∈N* , 且a1=1,求证:
(an+1+1),n∈N* , 且a1=1,求证:
(1)数列{an+2n}是等比数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com