
【题目】如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.

(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)欲证GH∥平面CDE,根据直线与平面平行的判定定理可知只需证GH与平面CDE内一直线平行,而G是AE,DF的交点,G是AE中点,又H是BE的中点,则GH∥AB,而AB∥CD,则GH∥CD,CD平面CDE,GH平面CDE,满足定理所需条件.(2)利用线面垂直的判定定理证明ED⊥面ABCD,即可证明面AFED⊥面ABCD
试题解析:(1)∵四边形ADEF是正方形,G是AE,DF的交点,
∴G是AE中点,
又H是BE的中点,
∴△EAB中,GH∥AB,
∵ABCD为平行四边形
∴AB∥CD
∴GH∥CD,
又∵CD平面CDE,GH平面CDE
∴GH∥平面CDE
(2)∵BD⊥平面CDE,
∴BD⊥ED,
∵四边形AFED为正方形,∴ED⊥AD,
∵AD∩BD=D,ED⊥面ABCD,
∵ED面AFED,
∴面AFED⊥面ABCD.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _________,
_________, ![]() __________,
__________, ![]() _________.
_________.
猜想: ![]() _______.
_______.
然后用数学归纳法证明.证明过程如下:
①当![]() 时,________________,猜想成立
时,________________,猜想成立
②假设![]() (
(![]() N*)时,猜想成立,即
N*)时,猜想成立,即![]() _______.
_______.
那么,当![]() 时,由已知
时,由已知![]() ,得
,得![]() _________.
_________.
又![]() ,两式相减并化简,得
,两式相减并化简,得![]() _____________(用含
_____________(用含![]() 的代数式表示).
的代数式表示).
所以,当![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何![]() N*都成立.
N*都成立.
思路2:先设![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出![]() _____________.
_____________.
由已知![]() ,写出
,写出![]() 与
与![]() 的关系式:
的关系式: ![]() _____________________,
_____________________,
两式相减,得![]() 与
与![]() 的递推关系式:
的递推关系式: ![]() ____________________.
____________________.
整理: ![]() ____________.
____________.
发现:数列![]() 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.
得出:数列![]() 的通项公式
的通项公式![]() ____,进而得到
____,进而得到![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量![]() 的取值为不大于
的取值为不大于![]() 的非负整数值,它的分布列为:
的非负整数值,它的分布列为:
| 0 | 1 | 2 |
| n |
|
|
|
|
|
|
其中![]() (
(![]() )满足:
)满足: ![]() ,且
,且![]() .
.
定义由![]() 生成的函数
生成的函数![]() ,令
,令![]() .
.
(I)若由![]() 生成的函数
生成的函数![]() ,求
,求![]() 的值;
的值;
(II)求证:随机变量![]() 的数学期望
的数学期望![]() ,
, ![]() 的方差
的方差![]() ;
;
(![]() )
)
(Ⅲ)现投掷一枚骰子两次,随机变量![]() 表示两次掷出的点数之和,此时由
表示两次掷出的点数之和,此时由![]() 生成的函数记为
生成的函数记为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
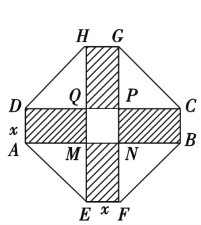
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com