练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在半径为40cm的半圆形（O为圆心）铝皮上截取一块矩形材料ABCD，其中A，B在直径上，点C，D在圆周上、
    （1）设AD=x，将矩形ABCD的面积y表示成x的函数，并写出其定义域；
    （2）怎样截取，才能使矩形材料ABCD的面积最大？并求出最大面积．

    【答案】
    （1）解：AB=2OA=2 =2 ，

    ∴y=f（x）=2x ，x∈（0，40）．


    （2）解：y2=4x2（1600﹣x2）≤4× =16002，即y≤1600，当且仅当x=20 时取等号．

    ∴截取AD=20 时，才能使矩形材料ABCD的面积最大，最大面积为1600．


    【解析】（1）OA=2 =2 ，可得y=f（x）=2x ，x∈（0，40）．（2）平方利用基本不等式的性质即可得出．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD． （Ⅰ）证明：PA⊥BD；
    （Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．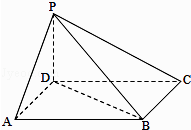

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定椭圆C： + =1（a＞b＞0），称圆C1：x2+y2=a2+b2为椭圆C的“伴随圆”．已知椭圆C的离心率为 ，且经过点（0，1）．
    （1）求实数a，b的值；
    （2）若过点P（0，m）（m＞0）的直线l与椭圆C有且只有一个公共点，且l被椭圆C的伴随圆C1所截得的弦长为2 ，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中正确的有 ．
    ①常数数列既是等差数列也是等比数列；
    ②在△ABC中，若sin2A+sin2B=sin2C，则△ABC为直角三角形；
    ③若A，B为锐角三角形的两个内角，则tanAtanB＞1；
    ④若Sn为数列{an}的前n项和，则此数列的通项an=Sn﹣Sn﹣1（n＞1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】大学生村官王善良落实政府“精准扶贫”精神，帮助贫困户张三用9万元购进一部节能环保汽车，用于出租．假设第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加2万元，该车每年的运营收入均为11万元．若该车使用了n（n∈N*）年后，年平均盈利额达到最大值，则n等于（注：年平盈利额=（总收入﹣总成本）× ）（ ）
    A.3
    B.4
    C.5
    D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数φ（x）=a2x﹣ax（a＞0，a≠1）．
    （1）求函数φ（x）在[﹣2，2]上的最大值；
    （2）当a= 时，φ（x）≤t2﹣2mt+2对所有的x∈[﹣2，2]及m∈[﹣1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知P为△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，PH⊥平面 ABC，H，则H为△ABC的（ ）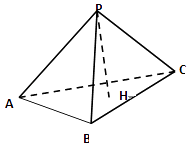
    A.重心
    B.垂心
    C.外心
    D.内心

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，过E点做EF⊥PB交PB于点F．求证：
    （1）PA∥平面DEB；
    （2）PB⊥平面DEF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，体积为 ，底面是边长为 的正三角形，若P为底面A1B1C1的中心，则PA与平面A1B1C1所成角的大小为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案