
【题目】已知函数![]()
![]() ,
,
(1)若曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,求
,求![]() 的值;
的值;
(2)讨论函数![]() 的单调性;
的单调性;
(3)设函数![]() ,若至少存在一个
,若至少存在一个![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;
(2)当![]()
![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]()
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() .
.
(3)![]()
【解析】
试题分析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,可得到
,可得到![]() 的值,可得
的值,可得![]() 的值;(2)
的值;(2)![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论
三种情况讨论![]() 的单调性;(3)若至少存在一个
的单调性;(3)若至少存在一个![]() ,使得
,使得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴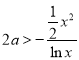 有解,令
有解,令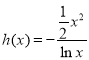 ,讨论函数
,讨论函数![]() 的性质,可得到
的性质,可得到
实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
∴![]() ,
,![]()
解得![]() ,∴
,∴![]() .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]()
当![]() 时,由
时,由![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
当![]() 时,由
时,由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() ,
,![]()
由![]() ,∴
,∴![]() 的单调减区间为
的单调减区间为![]() .
.
综上所述:当![]() 时,
时, ![]() ,∴
,∴![]() 的单调增区间为
的单调增区间为![]() ,
,
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]()
当![]() 时,∴
时,∴![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,
,![]() 的单调减区间为
的单调减区间为![]() .
.
(3)若至少存在一个![]() ,使得
,使得![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,∴
,∴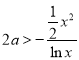 有解,令
有解,令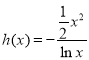 ,
,
∴![]()
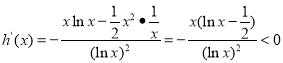 ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,![]()
∴![]() 得,
得,![]() .
.


科目:高中数学 来源: 题型:
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”、“演讲社”三个金牌社团中抽6人组成社团管理小组,有关数据见下表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求![]() 的值;
的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
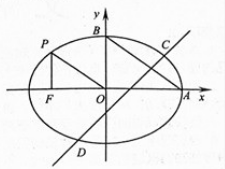
【题目】如图,过椭圆![]() 上一点
上一点![]() 向
向![]() 轴作垂线,垂足为左焦点
轴作垂线,垂足为左焦点![]() ,
,![]() 分别为
分别为![]() 的右顶点,上顶点,且
的右顶点,上顶点,且![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为
为![]() 上的两点,若四边形
上的两点,若四边形![]()
![]() 逆时针排列)的对角线
逆时针排列)的对角线![]() 所在直线的斜率为
所在直线的斜率为![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为a,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD,底面ABCD是边长为2的蓌形,PA⊥平面ABCD,PA=2,∠ABC=60°,E,F分别是BC,PC的中点。
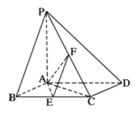
(1)求证:AE⊥PD;
(2)求二面角E-AF-C的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
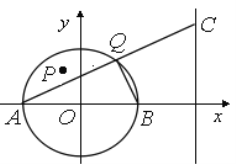
【题目】已知圆![]() ,直线
,直线![]() :x=6,圆
:x=6,圆![]() 与
与![]() 轴相交于点
轴相交于点![]() (如图),点P(-1,2)是圆
(如图),点P(-1,2)是圆![]() 内一点,点
内一点,点![]() 为圆
为圆![]() 上任一点(异于点
上任一点(异于点![]() ),直线
),直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)若过点P的直线![]() 与圆
与圆![]() 相交所得弦长等于
相交所得弦长等于![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地参加2015 年夏令营的![]() 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为![]() ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为![]() 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为![]() ,已知这
,已知这![]() 名学生分住在三个营区,从
名学生分住在三个营区,从![]() 到
到![]() 在第一营区,从
在第一营区,从![]() 到
到![]() 在第二营区,从
在第二营区,从![]() 到
到![]() 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com