
分析 (1)设等差数列{bn}的公差为d,则Pn(an,bn)(n∈N*)在函数y=log${\;}_{\frac{1}{2}}$x的图象上.${b}_{n}=lo{g}_{\frac{1}{2}}{a}_{n}$,可得an=$(\frac{1}{2})^{{b}_{n}}$.计算$\frac{{a}_{n+1}}{{a}_{n}}$为常数即可得出.
(2)由Sn=1-2-n,可得${a}_{1}=1-{2}^{-1}$=$\frac{1}{2}$.n≥2时,an=Sn-Sn-1=$(\frac{1}{2})^{n}$.可得bn=n.由Pn$((\frac{1}{2})^{n},n)$,Pn+1$((\frac{1}{2})^{n+1},n+1)$.过点Pn,Pn+1的直线方程为:$\frac{y-n}{(n+1)-n}$=$\frac{x-\frac{1}{{2}^{n}}}{\frac{1}{{2}^{n+1}}-\frac{1}{{2}^{n}}}$,可得:An$(\frac{n+2}{{2}^{n+1}},0)$,Bn(0,n+2).${c}_{n}=\frac{1}{2}|OA|•|OB|$.判定数列{cn}单调性即可得出.
解答 (1)证明:设等差数列{bn}的公差为d,则Pn(an,bn)(n∈N*)在函数y=log${\;}_{\frac{1}{2}}$x的图象上.
${b}_{n}=lo{g}_{\frac{1}{2}}{a}_{n}$,∴an=$(\frac{1}{2})^{{b}_{n}}$.
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$(\frac{1}{2})^{{b}_{n+1}-{b}_{n}}$=$(\frac{1}{2})^{d}$对n∈N*恒成立,
得到数列{an}是等比数列.
(2)解:由Sn=1-2-n,可得${a}_{1}=1-{2}^{-1}$=$\frac{1}{2}$.n≥2时,an=Sn-Sn-1=1-2-n-(1-2-(n-1))=$(\frac{1}{2})^{n}$.
${b}_{n}=lo{g}_{\frac{1}{2}}{a}_{n}$=$lo{g}_{\frac{1}{2}}(\frac{1}{2})^{n}$=n,
∴Pn$((\frac{1}{2})^{n},n)$,Pn+1$((\frac{1}{2})^{n+1},n+1)$.过点Pn,Pn+1的直线方程为:$\frac{y-n}{(n+1)-n}$=$\frac{x-\frac{1}{{2}^{n}}}{\frac{1}{{2}^{n+1}}-\frac{1}{{2}^{n}}}$,化为:y=n-2(2nx-1).
可得:An$(\frac{n+2}{{2}^{n+1}},0)$,Bn(0,n+2).${c}_{n}=\frac{1}{2}|OA|•|OB|$=$\frac{(n+2)^{2}}{{2}^{n+2}}$.
由cn-cn+1=$\frac{(n+2)^{2}}{{2}^{n+2}}-\frac{(n+3)^{2}}{{2}^{n+3}}$=$\frac{{n}^{2}+2n-1}{{2}^{n+2}}$>0.∴数列{cn}单调递减,
使得对任意的n∈N*,cn≤t恒成立,则t≥c1=$\frac{9}{8}$.
∴t的最小值为$\frac{9}{8}$.
点评 本题考查了数列递推关系、直线方程、数列的单调性、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,log2(3x+1)>0 | B. | ¬p:?x∈R,log2(3x+1)>0 | ||
| C. | ¬p:?x∈R,log2(3x+1)≤0 | D. | ¬p:?x∈R,log2(3x+1)≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组(重量) | [75,85) | [85,95) | [95,105) | [105,115) |
| 频数(个) | 15 | 30 | 35 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
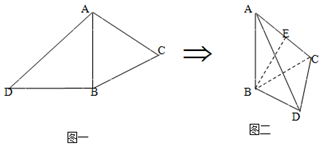 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
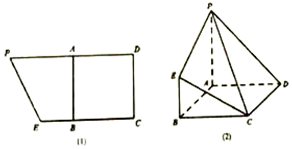 已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com