
【题目】已知函数f(x)=x3﹣3x2+1.
(1)求f(x)在x=1处的切线方程;
(2)求f(x)的极值;
(3)若方程f(x)=a+2有两个不相等的实数根,求a.
【答案】(1)3x+y﹣2=0; (2)极大值为1,极小值﹣3; (3)﹣1或﹣5
【解析】
(1)求出![]() ,进而求出
,进而求出![]() ,即可求出切线的点斜式方程;
,即可求出切线的点斜式方程;
(2)令![]() ,求出方程的解,进而求出函数的单调区间,即可求出结论;
,求出方程的解,进而求出函数的单调区间,即可求出结论;
(3)根据(2)的结论做出![]() 的图像,转化为
的图像,转化为![]() 与
与![]() 有两个交点,数形结合,即可求出结论.
有两个交点,数形结合,即可求出结论.
解:(1)![]() =3x2﹣6x,∴
=3x2﹣6x,∴![]() =312﹣61=﹣3,
=312﹣61=﹣3,
而f(1)=13﹣312+1=﹣1,
∴f(x)在x=1处的切线方程:y+1=﹣3(x﹣1),即3x+y﹣2=0;
所以f(x)在x=1处的切线方程:3x+y﹣2=0;
(2),由(1)得,f'(x)=0,x=0,或x=2,
x∈(﹣∞,0)和(2,+∞),f'(x)>0,x∈(0,2),f'(x)<0,
即![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() ,
,
所以极大值f(0)=1,极小值f(2)=﹣3,
所以函数的极大值为1,极小值﹣3;
(3)方程f(x)=a+2有两个不相等的实数根,
即![]() 与直线
与直线![]() 有两个交点,
有两个交点,
做出函数![]() 如下图所示,
如下图所示,
当![]() 或
或![]() ,即
,即![]() 或
或![]() 时,
时,
![]() 有两个不相等的实数根.
有两个不相等的实数根.



 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 距离比它到直线
距离比它到直线![]() 距离少1.
距离少1.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)记动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() ,延长
,延长![]() ,
,![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试探究
,试探究![]() 是否为定值?若为定值,请求出定值,若不为定值,请说明理由.
是否为定值?若为定值,请求出定值,若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.命题“若am2<bm2,则a<b”的逆命题是真命题
B.命题“存在x0∈R,x02﹣x0>0”的否定是“对任意的xR,x2﹣x≤0”
C.命题“p或q”为真命题,则命题p和命题q均为真命题
D.已知函数f(x)在R上可导,则f'(x0)=0是f(x0)为函数f(x)的极值”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点O与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),直线l:
),直线l:![]() ,若直线l与曲线C相交于A,B两点,且
,若直线l与曲线C相交于A,B两点,且![]() .
.
(1)求a;
(2)若M,N为曲线C上的两点,且![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且(a+b﹣c)(sinA+sinB+sinC)=bsinA.
(1)求C;
(2)若a=2,c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,xn+1=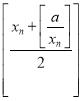 (n∈N*).现有下列命题:
(n∈N*).现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>![]() -1;
-1;
④对某个正整数k,若xk+1≥xk,则xk=[![]() ].
].
其中的真命题有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() >
>![]() >0
>0![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点![]() 作直线
作直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 都只有一个交点.求证:
都只有一个交点.求证:![]() ⊥
⊥![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com