
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
科目:高中数学 来源: 题型:
【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12. 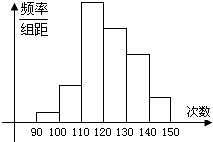
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:以点C(t, ![]() )(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)当t=2时,求圆C的方程;
(2)求证:△OAB的面积为定值;
(3)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4且t≠![]() ;
;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<![]() .
.
其中正确的命题是________(把所有正确命题的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com