
已知指数函数f(x)的图象经过点(3,8),求f(1)、f(-1)、f(2x-3)的值.
解:设指数函数y=ax(a>0,a≠1),因为函数f(x)的图象经过点(3,8),
所以,f(3)=8,即a3=8,解得a=2,于是有,f(x)=2x.
所以,f(1)=21=2,f(-1)=2-1=![]() ,f(2x-3)=22x-3.
,f(2x-3)=22x-3.
点评:本题要弄清两点,一是指数函数的形式即函数的解析式为y=ax(a>0,a≠1),二是求解析式字母a的值,只需要有一个条件即可.另外对于求函数值的问题,必须是以已知函数解析式为前提,才能求函数的值.
要求f(1)、f(-1)、f(2x-3)的值,必须要先求出指数函数f(x)的解析式,根据定义,指数函数的解析式为y=ax(a>0,a≠1),因此,本题就是求底数a的值,把底数a的值求出后,f(1)、f(-1)、f(2x-3)的值也就迎刃而解了.


科目:高中数学 来源: 题型:013
已知指数函数f(x)=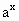 ,g(x)=
,g(x)= .(a,b>0且a,b≠1)的反函数分别为
.(a,b>0且a,b≠1)的反函数分别为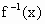 ,
,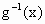 ,若lga+lgb=0,则y=
,若lga+lgb=0,则y= 与y=
与y=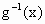 的图象
的图象
[ ]
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:022
已知指数函数f(x)=ax的图像经过点(3,8),则f(-1)的值为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com