
分析 (1)利用初等变换能求出矩阵M的逆矩阵M-1.
(2)将曲线|x|+|y|=1在矩阵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$对应的变换作用进行化简,能求出曲线C的方程.
(3)作出曲线C所围成的图形即可得到结论.
解答 解: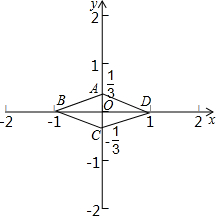 (1)∵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$,
(1)∵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$,
∴[M|I]=$[\begin{array}{l}{1}&{0}&{\;}&{1}&{0}\\{0}&{\frac{1}{3}}&{\;}&{0}&{1}\end{array}]$→$[\begin{array}{l}{1}&{0}&{\;}&{1}&{0}\\{0}&{1}&{\;}&{0}&{3}\end{array}]$,
∴矩阵M的逆矩阵M-1=$[\begin{array}{l}{1}&{0}\\{0}&{3}\end{array}]$.
(2)设曲线|x|+|y|=1上(x0,y0)在矩阵M=$[{\begin{array}{l}1&0\\ 0&{\frac{1}{3}}\end{array}}]$
对应的变换作用下得到的曲线对应点为(x,y),
∴$[\begin{array}{l}{1}&{0}\\{0}&{\frac{1}{3}}\end{array}]$$[\begin{array}{l}{{x}_{0}}\\{{y}_{0}}\end{array}]$=$[\begin{array}{l}{x}\\{y}\end{array}]$,即x0=x,y0=3y,
代入|x|+|y|=1中得:|x|+|3y|=1,
∴曲线C方程为:|x|+|3y|=1.
(3)∵|x|+|3y|=1,
∴当x≥0,y≥0时,方程等价于x+3y=1;
当x≥0,y≤0时,方程等价于x-3y=1;
当x≤0,y≥0时,方程等价于-x+3y=1;
当x≤0,y≤0时,方程等价于-x-3y=1,
其图象为菱形ABCD,
则曲线C所围成图形的面积为S=$\frac{1}{2}$×2×$\frac{2}{3}$=$\frac{2}{3}$.
点评 此题考查了几种特殊的矩形变换,确定出变换后的曲线方程是解本题的关键,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-2,\left.{-\frac{1}{3}}]$ | B. | $(-2,\left.{\frac{1}{2}}]$ | C. | $(-\frac{1}{3},\left.{\frac{1}{2}}]$ | D. | $(-1,\left.{\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<2ef(2) | B. | ef(1)<f(2) | C. | f(1)<0 | D. | ef(e)<2f(2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com