
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
(Ⅰ)将两圆方程相减可得一直线方程l:x+y-4=0,该直线叫做这两圆的“根轴”,试证点P落在根轴上;
(Ⅱ)求切线长|PA|的最小值;
 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
⑴ ![]()
即点P(a,b)落在根轴l:x+y-4=0上; …………………… 3分
⑵ ![]()
![]()
∴当a=2时即P为(2,2)点时有![]() ………………… 6分
………………… 6分
 ⑶ 作M(0,2)关于直线L: x+y=4的对称点N,求得N(2,4),连接NO则NO分别与直线L、圆O的交点即为使|PM|+|PQ|的值最小的点P、Q; ………………… 8分
⑶ 作M(0,2)关于直线L: x+y=4的对称点N,求得N(2,4),连接NO则NO分别与直线L、圆O的交点即为使|PM|+|PQ|的值最小的点P、Q; ………………… 8分
证明如下:
在L上任取不同于点P的P1点,
连接P1O交圆O于Q1,则
|P1M|+|P1Q1|=|P1M|+|P1O|-1=|P1N|+|P1O|-1>|NO|-1
而|PM|+|PQ|=|PM|+|PO|-1=|PN|+|PO|-1=|NO|-1 ,
故得证; …………… 11分
下求|PM|+|PQ|的最小值及点P的坐标:
(|PM|+|PQ|)Min=|NO|-1=![]()
联立ON与直线L的方程可得![]() …… 13分
…… 13分


科目:高中数学 来源:辽宁省沈阳二中2011-2012学年高二上学期期中考试数学文科试题 题型:013
已知圆O:x2+y2=1,点P在直线![]() 上,O为坐标原点,若圆O上存在点Q,使∠OPQ=30°,则点P的纵坐标y0的取值范围是
上,O为坐标原点,若圆O上存在点Q,使∠OPQ=30°,则点P的纵坐标y0的取值范围是
[-2,2]
[0,2]
[-1,1]
[0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
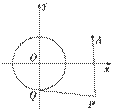
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.

(1)求a、b间关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
(1)求a、b间关系;
(2)求|PQ|的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=1,圆C:(x-2)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|.
(1)求实数a、b间满足的![]() 等量关系;
等量关系;
(2)求切线长|PA|的最小值;
(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com