
【题目】五边形![]() 是由一个梯形
是由一个梯形![]() 与一个矩形
与一个矩形![]() 组成的,如图甲所示,B为AC的中点,
组成的,如图甲所示,B为AC的中点, ![]() . 先沿着虚线
. 先沿着虚线![]() 将五边形
将五边形![]() 折成直二面角
折成直二面角![]() ,如图乙所示.
,如图乙所示.
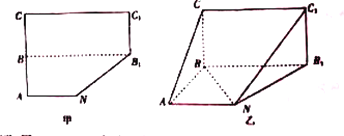
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求图乙中的多面体的体积.
【答案】(1)证明详见解析;(2)![]() .
.
【解析】试题分析:本题主要考查线线垂直、线面垂直、面面垂直、锥体的体积等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力.第一问,由四边形![]() 为矩形,得
为矩形,得![]() ,再由直二面角,得
,再由直二面角,得![]() ,再由勾股定理得
,再由勾股定理得![]() ,利用线面垂直的判定,得
,利用线面垂直的判定,得![]()
![]() ,最后利用面面垂直的判定,得平面
,最后利用面面垂直的判定,得平面![]() 平面
平面![]() ;第二问,把图乙中的多面体拆成两个几何体,一个是锥体
;第二问,把图乙中的多面体拆成两个几何体,一个是锥体![]() ,一个是锥体
,一个是锥体![]() ,利用锥体体积公式分别计算,再求和即可.
,利用锥体体积公式分别计算,再求和即可.
试题解析:(1)证明:四边形![]() 为矩形,故
为矩形,故![]() ,又由于二面角
,又由于二面角![]() 为直二面角,故
为直二面角,故![]() ,故
,故![]() ,
,
由线段![]() 易知,
易知, ![]() ,
,
即![]() ,因此
,因此![]()
![]() ,
,
所以平面![]()
![]() ;(5分)
;(5分)
(2)解:连接CN,过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,且平面
,且平面![]()
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]()
此几何体的体积![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)令![]() ,其图象上任意一点
,其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 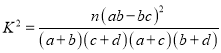 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+![]() x2+mx在x=1处有极小值,
x2+mx在x=1处有极小值,
g(x)=f(x)﹣![]() x3﹣
x3﹣![]() x2+x﹣alnx.
x2+x﹣alnx.
(1)求函数f(x)的单调区间;
(2)是否存在实数a,对任意的x1、x2∈(0,+∞),且x1≠x2,有![]() 恒成立?若存在,求出a的取值范围;若不存在,说明理由.
恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若点![]() 的横坐标为1,求
的横坐标为1,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知直线l经过点![]() ,倾斜角
,倾斜角![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线l的参数方程,并把圆![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)设l与圆![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)将分别于2017年3月5日和3月3日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与者中随机选出200人,并将这200人按年龄分组:第
.现从参与者中随机选出200人,并将这200人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:

(1)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有![]() 人年龄在第3组的概率;
人年龄在第3组的概率;
(2)若从所有参与调查的人(人数很多)中任意选出3人,记关注民生问题的人数为X,求X的分布列与期望;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的人中老年人有10人,问是否有![]() 的把握认为是否关注民生问题与年龄有关?
的把握认为是否关注民生问题与年龄有关?
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
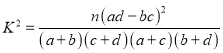 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,设
上,设![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)如图所示,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 为
为![]() 中点,过
中点,过![]() 作与直线
作与直线![]() 垂直的直线
垂直的直线![]() ,证明:对于任意的
,证明:对于任意的![]() ,直线
,直线![]() 恒过定点,并求出此定点坐标.
恒过定点,并求出此定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com