
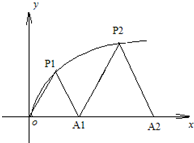
 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉ ЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉ ЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ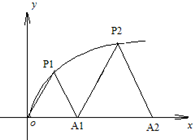 НтЃКЃЈ1ЃЉвРЬтвтЃЌOP1жБЯпЗНГЬЮЊy=
НтЃКЃЈ1ЃЉвРЬтвтЃЌOP1жБЯпЗНГЬЮЊy=| 3 |
| 3 |
| 3 |
| an-1+an |
| 2 |
| 3 |
| 3 |
| 3 |
| an-1+an |
| 2 |
| 3 |
| an-an-1 |
| 2 |
| 3 |
| an-an-1 |
| 2 |
| 3 |
| 2 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
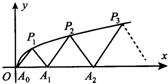 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎдђa1=
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎдђa1=ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ
ШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЁЂP2ЃЈx2ЃЌy2ЃЉЁЂЁЁЂPnЃЈxnЃЌynЃЉЃЈ0ЃМy1ЃМy2ЃМЁЃМynЃЉЪЧЧњЯпCЃКy2=3xЃЈyЁн0ЃЉЩЯЕФnИіЕуЃЌЕуAiЃЈaiЃЌ0ЃЉЃЈi=1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉдкxжсЕФе§АыжсЩЯЃЌЧвЁїAi-1AiPiЪЧе§Ш§НЧаЮЃЈA0ЪЧзјБъдЕуЃЉЃЎ| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
| 1 |
| 6 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
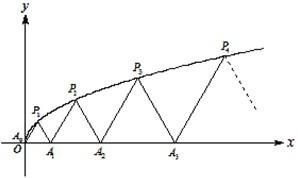
 ЃЈ2012•еЂББЧјЖўФЃЃЉШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЪЧЧњЯпCЃКy2=
ЃЈ2012•еЂББЧјЖўФЃЃЉШчЭМЃЌP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЁЃЌPnЃЈxnЃЌynЃЉЃЌЁЪЧЧњЯпCЃКy2=| 1 |
| 2 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com