
【题目】已知x,y满足约束条件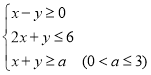 ,当
,当![]() 时,
时,![]() 的最小值是________.若
的最小值是________.若![]() 的最大值是-1,则
的最大值是-1,则![]() ________.
________.
【答案】3 2
【解析】
![]() 时画出约束条件
时画出约束条件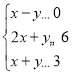 表示的平面区域,作直线
表示的平面区域,作直线![]() ,将直线
,将直线![]() 在不等式组表示的平面区域内平移,由数形结合求得最优解,计算
在不等式组表示的平面区域内平移,由数形结合求得最优解,计算![]() 的最小值;画出约束条件
的最小值;画出约束条件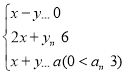 表示的平面区域,作直线
表示的平面区域,作直线![]() ,将直线
,将直线![]() 在不等式组表示的平面区域内平移,由数形结合求出最优解,计算
在不等式组表示的平面区域内平移,由数形结合求出最优解,计算![]() 的最大值.
的最大值.
当![]() 时,画出约束条件
时,画出约束条件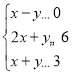 表示的平面区域,如图所示;
表示的平面区域,如图所示;
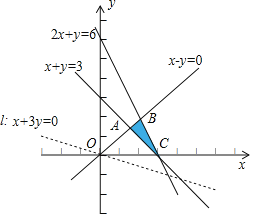
作直线![]() ,将直线
,将直线![]() 在不等式组表示的平面区域内平移,
在不等式组表示的平面区域内平移,
由数形结合知,当直线过点![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距最小,此时
轴上的截距最小,此时![]() 最小,
最小,
由![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
此时![]() 的最小值为
的最小值为![]() .
.
画出约束条件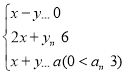 表示的平面区域,如图所示;
表示的平面区域,如图所示;
作直线![]() span>,将直线
span>,将直线![]() 在不等式组表示的平面区域内平移,
在不等式组表示的平面区域内平移,
由数形结合知,当直线过点![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距最大,此时
轴上的截距最大,此时![]() 最大,
最大,
由![]() ,解得
,解得![]() ,所以
,所以![]() ,
,![]() ,
,
此时![]() 的最大值为
的最大值为![]() ,解得
,解得![]() .
.
故答案为:3,2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】十五巧板,又称益智图,为清朝浙江省德清知县童叶庚在同治年间所发明,它能拼出草木、花果、鸟兽、鱼虫、文字等图案.十五巧板由十五块板组成一个大正方形(如图1),其中标号为![]() 的小板为等腰直角三角形,图
的小板为等腰直角三角形,图![]() 是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )
是用十五巧板拼出的2019年生肖猪的图案,则从生肖猪图案中任取一点,该点恰好取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)若bn=![]() ,且数列{bn}的前
,且数列{bn}的前![]() 项和为Sn=360,求
项和为Sn=360,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小形状完全相同的![]() 个乒乓球,其中1个乒乓球上标有数字1,2个乒乓球上标有数字2,其余
个乒乓球,其中1个乒乓球上标有数字1,2个乒乓球上标有数字2,其余![]() 个乒乓球上均标有数字3
个乒乓球上均标有数字3![]() ,若从这个口袋中随机地摸出2个乒乓球,恰有一个乒乓球上标有数字2的概率是
,若从这个口袋中随机地摸出2个乒乓球,恰有一个乒乓球上标有数字2的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)从口袋中随机地摸出2个乒乓球,设![]() 表示所摸到的2个乒乓球上所标数字之积,求
表示所摸到的2个乒乓球上所标数字之积,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
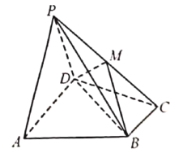
【题目】如图,线段![]() 是等腰
是等腰![]() 的一条中位线,
的一条中位线,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() .现将
.现将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() .
.
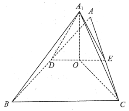
(1)求证:![]() ;
;
(2)探究:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,请指出点
,若存在,请指出点![]() 的位置并说明理由.若不存在,请说明理由.
的位置并说明理由.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从30个个体中抽取10个个体,并将这30个个体编号00,01,…,29.现给出某随机数表的第11行到第15行(见下表),如果某人选取第12行的第6列和第7列中的数作为第1个数并且由此数向右读,则选取的前4个的号码分别为( )
9264 | 4607 | 2021 | 3920 | 7766 | 3817 | 3256 | 1640 |
5858 | 7766 | 3170 | 0500 | 2593 | 0545 | 5370 | 7814 |
2889 | 6628 | 6757 | 8231 | 1589 | 0062 | 0047 | 3815 |
5131 | 8186 | 3709 | 4521 | 6665 | 5325 | 5383 | 2702 |
9055 | 7196 | 2172 | 3207 | 1114 | 1384 | 4359 | 4488 |
A.76,63,17,00B.16,00,02,30C.17,00,02,25D.17,00,02,07
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着
绕着![]() 翻折到
翻折到![]() .
.
(1)![]() 为
为![]() 上一点,且
上一点,且![]() ,当
,当![]() 平面
平面![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)当平面![]() 与平面
与平面![]() 所成的锐二面角大小为
所成的锐二面角大小为![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦.
所成角的正弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: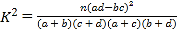 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中所有棱长都相等,
中所有棱长都相等,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.现有下列四个结论:
的中点.现有下列四个结论:
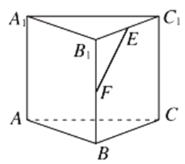
![]() ;
;![]() ;
;
![]() 平面
平面![]() ;
;![]() 异面直线
异面直线![]() 与
与![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
其中正确的结论是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com