
【题目】某超市计划按月订购一种酸奶,每天进货量相同,已知每售出一箱酸奶的利润为50元,当天未售出的酸奶降价处理,以每箱亏损10元的价格全部处理完.若供不应求,可从其它商店调拨,每销售1箱可获利30元.假设该超市每天的进货量为14箱,超市的日利润为![]() 元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
元.为确定以后的订购计划,统计了最近50天销售该酸奶的市场日需求量,其频率分布表如图所示.
序号 | 分组 | 频数(天) | 频率 |
1 |
|
| 0.16 |
2 |
| 12 |
|
3 |
|
| 0.3 |
4 |
|
|
|
5 |
| 5 | 0.1 |
合计 | 50 | 1 | |
(1)求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 关于日需求量
关于日需求量![]() 的函数表达式;
的函数表达式;
(3)以50天记录的酸奶需求量的频率作为酸奶需求量发生的概率,估计日利润在区间![]() 内的概率.
内的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为:
 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.
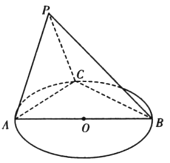
(1)证明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为
与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为![]()

(1)求椭圆![]() 的离心率;
的离心率;
(2) 设点C、D、F2分别为椭圆![]() 的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆
的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆![]() 相交于M、N 两点,若
相交于M、N 两点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线Cn:x2﹣2nx+y2=0,(n=1,2,…).从点P(﹣1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn).
(1)求数列{xn}与{yn}的通项公式;
(2)证明: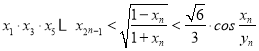 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com