
分析 (Ⅰ)先对函数f(x)进行求导,根据 f'(1)=0,f'(3)=24确定函数的解析式,然后令f'(x)<0求单调递减区间;
(Ⅱ)把a=1代入函数f(x)后对函数进行求导,由题意可得f′(x)=3x2+b≤0在[-1,1]上恒成立,分离参数b得答案.
解答 解:(Ⅰ)已知函数f(x)=ax3+bx(x∈R),∴f′(x)=3ax2+b,
又函数f(x)图象在点x=3处的切线与直线24x-y+1=0平行,
且函数f(x)在x=1处取得极值,∴f′(3)=27a+b=24,
且f′(1)=3a+b=0,解得a=1,b=-3,
∴f(x)=x3-3x.
令f′(x)=3x2-3≤0,得-1≤x≤1,
∴函数的单调递减区间为[-1,1]
(Ⅱ)当a=1时,f(x)=x3+bx(x∈R),又函数f(x)在[-1,1]上是减函数,
∴f′(x)=3x2+b≤0在[-1,1]上恒成立.
即b≤-3x2在[-1,1]上恒成立,∴b≤-3.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,属中档题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8] | B. | (-∞,-8) | C. | (-∞,-6] | D. | (-∞,-6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
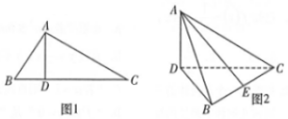 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com