
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 在点
在点![]() 处的切线与函数
处的切线与函数![]() 相切.
相切.
(1)求函数![]() 的值域;
的值域;
(2)求证:![]() .
.
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 是椭圆
是椭圆![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考前回归课本复习过程中,一数学老师在黑板上写了下面四个函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .然后说了四句话:第一句:“该函数定义域为
.然后说了四句话:第一句:“该函数定义域为![]() ,还是奇函数”.第二句:“该函数为偶函数,值域不是
,还是奇函数”.第二句:“该函数为偶函数,值域不是![]() ”.第三句:“该函数定义域为
”.第三句:“该函数定义域为![]() ,还是单调函数”.第四句:“该函数的图象有对称轴,值域是
,还是单调函数”.第四句:“该函数的图象有对称轴,值域是![]() ”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
”,若老师的每一句话只说对了一半,则这四个函数中符合老师说的所有函数的编号为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地开发一片荒地,如图,荒地的边界是以C为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE,OF,分别与荒地的边界有且仅有一个接触点A,B.现规划修建一条新路(由线段MP,![]() ,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,
,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,![]() 所对的圆心角为
所对的圆心角为![]() .记∠PCA=
.记∠PCA=![]() (道路宽度均忽略不计).
(道路宽度均忽略不计).
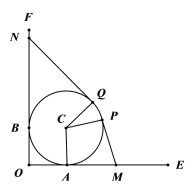
(1)若![]() ,求QN的长度;
,求QN的长度;
(2)求新路总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球,现从该箱中有放回地依次取出3个小球.则3个小球颜色互不相同的概率是_____;若变量ξ为取出3个球中红球的个数,则ξ的数学期望E(ξ)为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,E,M分别是BC,PD中点,点F在棱PC上移动.
,E,M分别是BC,PD中点,点F在棱PC上移动.
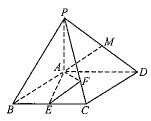
(1)证明无论点F在PC上如何移动,都有平面![]() 平面
平面![]() ;
;
(2)当直线AF与平面PCD所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为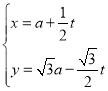 (t为参数,
(t为参数,![]() ).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点![]() 在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
(2)已知![]() ,点P在直线l上,点Q在曲线C上,且
,点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点F2是双曲线![]() 的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
A.8B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com