
【题目】如图,点![]() 为正方形边
为正方形边![]() 上异于点
上异于点![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,使得平面
,使得平面![]() 平面
平面![]() ,则下列说法中正确的是__________.(填序号)
,则下列说法中正确的是__________.(填序号)

(1)在平面![]() 内存在直线与
内存在直线与![]() 平行;
平行;
(2)在平面![]() 内存在直线与
内存在直线与![]() 垂直
垂直
(3)存在点![]() 使得直线
使得直线![]() 平面
平面![]()
(4)平面![]() 内存在直线与平面
内存在直线与平面![]() 平行.
平行.
(5)存在点![]() 使得直线
使得直线![]() 平面
平面![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)若该书每本的成本为![]() 元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: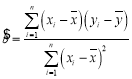
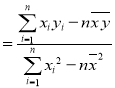 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅲ)当![]() 时,求四棱锥
时,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为![]() 的
的![]() 个个体组成,利用下面的随机数表选取
个个体组成,利用下面的随机数表选取![]() 个个体,选取方法是从随机数表第
个个体,选取方法是从随机数表第![]() 行的第
行的第![]() 列和第
列和第![]() 列数字开始由左到右依次选取两个数字,则选出来的第
列数字开始由左到右依次选取两个数字,则选出来的第![]() 个个体的编号为( )
个个体的编号为( )
7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了![]() 学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
组号 | 分组 | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
|
| 0.35 |
3 |
| 30 |
|
4 |
| 20 | 0.20 |
5 |
| 10 | 0.10 |
合计 | 100 | 1 | |
(1)求![]() 的值,并在答题卡上作出这些数据的频率分布直方图;(用阴影涂黑)
的值,并在答题卡上作出这些数据的频率分布直方图;(用阴影涂黑)
(2)根据频率分布直方图估计该组数据的众数及中位数(求中位数精确到![]() );
);
(3)现从第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人参加校“中华诗词比赛”,经过比赛后从这
人参加校“中华诗词比赛”,经过比赛后从这![]() 人中选拔
人中选拔![]() 人组成该校代表队,求这
人组成该校代表队,求这![]() 人来自不同组别的概率.
人来自不同组别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx(a∈R).
(1)若x=![]() 是函数f(x)的一个极值点,求实数a的值;
是函数f(x)的一个极值点,求实数a的值;
(2)当a>0时,讨论函数f(x)的单调性;
(3)当a>2且x>1时,求证:函数f(x)的最小值小于﹣3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个车间为了规定工时定额,需要确定加工某种零件所花费的时同,为此进行了6次试验,收集数据如下:
零件数x(个) | 1 | 2 | 3 | 4 | 5 | 6 |
加工时间y(小时) | 3.5 | 5 | 6 | 7.5 | 9 | 11 |
(1)在给定的坐标系中画出散点图,并指出两个变量是正相关还是负相关;
(2)求回归直线方程;
(3)试预测加工7个零件所花费的时间?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
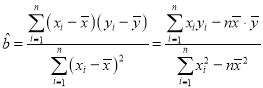 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com