
【题目】一生物科研小组对升高温度的多少与某种细菌种群存活数量之间的关系进行分析研究,他们制作5 份相同的样本并编号1、2、3、4、5,分别记录它们同在![]() 下升高不同的温度后的种群存活数量, 得到如下资料:
下升高不同的温度后的种群存活数量, 得到如下资料:
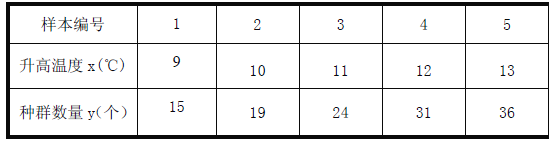
(1)若随机选取2份样本的数据来研究,求其编号不相邻的概率;
(2)求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)利用(2)中所求出的回归方程预测温度升高15 ![]() 时此种样本中种菌群存活数量.
时此种样本中种菌群存活数量.
附: 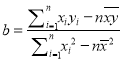 ,
, ![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据题意列举出从5组数据中选取2组数据共有10种情况,每种情况都是可能出现的,满足条件的事件包括的基本事件有6种.根据等可能事件的概率做出结果.(2)根据所给的数据,先做出x,y的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程并进行预报;
(3)根据回归方程令![]() 求值即可.
求值即可.
试题解析:
(1)总的选取结果为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10中,其中满足编号不相邻的有(1,3),(1,4),(1,5),(2,4),(2,5),(3,5)共6种,则概率为![]()
(2)由数据求得![]() ,
, ![]() ,则
,则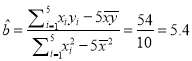
![]() ,所以y关于x的线性回归方程为
,所以y关于x的线性回归方程为![]()
(3)利用直线方程![]() ,可预测温度升高15℃时此种样本中细菌种群存活数量为
,可预测温度升高15℃时此种样本中细菌种群存活数量为![]()


科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn=2an﹣2,数列{bn}是首项为a1 , 公差不为零的等差数列,且b1 , b3 , b11成等比数列.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}满足cn= ![]() ,前n项和为Pn , 对于n∈N*不等式 Pn<t恒成立,求实数t的取值范围.
,前n项和为Pn , 对于n∈N*不等式 Pn<t恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
参考公式:  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点( ![]() ,
, ![]() ).
).
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣∞,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),离心率e=![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线l1:y=kx+m1与椭圆G交于 A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示.
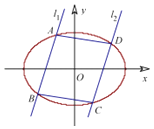
①证明:m1+m2=0;
②求四边形ABCD 的面积S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)都是定义在R上的函数,并满足:
1)f(x)=2axg(x),(a>0,a≠1);
2)g(x)≠0;
3)f(x)g′(x)<f′(x)g(x)且 ![]() +
+ ![]() =5,则a= .
=5,则a= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com