[题目]已知函数(I)若函数处取得极值.求实数的值,并求此时上的最大值,(Ⅱ)若函数不存在零点.求实数a的取值范围, 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数

(I)若函数处取得极值，求实数的值；并求此时上的最大值；

(Ⅱ)若函数不存在零点，求实数a的取值范围；

【答案】（1）最大值为；（2）实数的取值范围是。

【解析】试题分析：（1）根据函数的极值的概念得到，，根据函数的单调性得到函数的最值。（2）研究函数的单调性，找函数和轴的交点，使得函数和轴没有交点即可；分和，两种情况进行讨论。

解析：

（1）函数的定义域为R，，

， .

在上单调递减，在上单调递增，所以时取极小值.

所以所求实数的值为1.

易知在上单调递增，在上单调递减；

且 .

当时，在的最大值为

（2），由于.

①当时，是增函数，

且当时， .

当时，，，取，

则，所以函数存在零点.

②当时， .

在上单调递减，在上单调递增，所以时取最小值.

函数不存在零点，等价于，

解得.

综上所述：所求的实数的取值范围是.

练习册系列答案

远航教育口算题卡系列答案

扬帆文化100分培优智能优选卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数（）．

（1）讨论的单调性；

（2）当时，若函数的图象全部在直线的下方，求实数的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某中学举行一次“环保知识竞赛”，全校学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为分）作为样本进行统计，请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图（如图所示）解决下列问题：

（Ⅰ）写出，，，的值．

（Ⅱ）在选取的样本中，从竞赛成绩是分以上（含分）的同学中随机抽取名同学到广场参加环保知识的志愿宣传活动，求所抽取的名同学来自同一组的概率．

（Ⅲ）在（Ⅱ）的条件下，设表示所抽取的名同学中来自第组的人数，求的分布列及其数学期望．

组别	分组	频数	频率
第组
第组
第组
第组
第组
合计

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】选修4-5：不等式选讲

已知函数

（Ⅰ）求不等式的解集；

（Ⅱ）已知函数的最小值为，若实数且，求的

最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之，问各出几何？此问题的译文是:今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还，他们各应偿还多少？已知牛、马、羊的主人各应偿还升，升，升，1斗为10升，则下列判断正确的是( )

A. ，，依次成公比为2的等比数列，且

B. ，，依次成公比为2的等比数列，且

C. ，，依次成公比为的等比数列，且

D. ，，依次成公比为的等比数列，且

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某省电视台为了解该省卫视一档成语类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数(单位：千人)如下茎叶图所示，其中一个数字被污损．

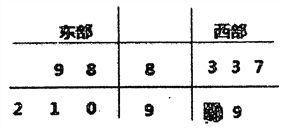
(I)求东部观众平均人数超过西部观众平均人数的概率.

(II)节目的播出极大激发了观众随机统计了4位观众的周均学习成语知识的的时间y (单位：小时)与年龄x(单位：岁)，并制作了对照表(如下表所示)：

由表中数据分析，x，y呈线性相关关系，试求线性回归方程，并预测年龄为60岁观众周均学习成语知识的时间．

参考数据：线性回归方程中的最小二乘估计分别是．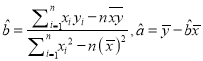

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂对一批产品进行了抽样检测，如图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106]．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是(　　)

A. 90 B. 75

C. 60 D. 45

查看答案和解析>>

科目：高中数学 来源： 题型：