练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设X是一个离散型随机变量，其分布列为：
    X
    		-1
    		0
    		1
    P
    		0.5
    		1-2q

     
    则q=         
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    如图，是当取不同值的三种正态曲线的图象，那么的关系是                                                                  （  ）
    、 、              
    、 、

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）有一牛奶商店每瓶牛奶进价为0.80元，售价为1元，但牛奶必须于每晚进货，于次日早晨出售；昨晚进货不多可能会因供不应求减少可得利润，若进货过多，次日早晨卖不完，则不能再隔夜出售（牛奶会发酸变质），每剩一瓶则造成0.80元的损失，过去的经验可以作为未来发展的参考，历史上200天的销售记录如下：
    日销售量
    		天数
    		概率
    25瓶
    		20
    		0.10
    26瓶
    		60
    		0.30
    27瓶
    		100
    		0.50
    28瓶
    		20
    		0.10
    在统计的这200天当中，从未发生日销24瓶以下或29瓶以上的情况，我们可以假定日销24瓶以下或29瓶以上的情形不会发生，或者说此类事情发生的概率为零.作为经销商应如何确定每日进货数.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题满分14分）第一题满分4分，第二题满分4分，第三题满分6分．
    甲乙二人用4张扑克牌（分别是红桃2，红桃3，红桃4，方片4）玩游戏，他们将4张扑克牌洗匀后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽一张。
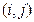    （1）设分别表示甲、乙抽到的牌的数字（方片4用4’表示，红桃2，红桃3，红桃4分别用2，3，4表示），写出甲乙二人抽到的牌的所有情况；
    （2）若甲抽到红桃3，则乙抽出的牌的牌面数字比3大的概率是多少？
    （3）甲乙约定：若甲抽到的牌的牌面数字比乙大，则甲胜；若甲抽到的牌的牌面数字不比乙大，则乙胜。你认为此游戏是否公平，说明你的理由。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
    已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作．
    （1）若每名志愿者在5天中任选一天参加社区服务工作，且各志愿者的选择互不影响，求3名志原者恰好连续3天参加社区服务工作的概率；
    （2）若每名志愿者在这5天中任选两天参加社区服务工作，且各志愿者的选择互不影响，记表示这3名志愿者在10月1号参加志愿者服务工作的人数，求随机变量的数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）甲有一个装有个红球、个黑球的箱子，乙有一个装有个红球、个黑球的箱子，两人各自从自己的箱子里任取一球，并约定:所取两球同色时甲胜，异色时乙胜（，，，）．
    (Ⅰ)当,时，求甲获胜的概率；
    （Ⅱ）当，时，规定：甲取红球获胜得3分；取黑球获胜得1分；甲负得0分．求甲的得分期望达到最大时的，值；
    （Ⅲ）当时，这个游戏规则公平吗？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    要从10名女生与5名男生中选出6名学生组成课外活动小组，如果按性别依比例分层随机抽样，试问组成此课外学习小组的概率为（　　）
    Ａ．     Ｂ．    C．    D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某人有5把钥匙，其中2把能打开门，现随机取1把钥匙试着开门，不能开门就扔掉，现采用随机模拟的方法估计第三次才能打开门的概率：先由计算器产生1~5之间的整数随机数，1,2表示能打开门，3,4,5表示打不开门，再以每三个数一组，代表三次开门的结果，经随机模拟产生了20组随机数，453,254,341,134,543,623,452,324,534,435,635,314,245,
    531,351,354,345,413,425,653据此估计，该人第三次才打开门的概率（    ）
    A  0.2      B.  0.25     C.  0.15        D.   0.35

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设随机变量～，～，若，则
                

    查看答案和解析>>

    同步练习册答案