练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．设曲线f（x）=2mx-ln（x+1）在点（0，0）处的切线方程为y=3x，则m的值为（　　）
    A．1B．-1C．2D．-2

    分析 根据导数的几何意义，即f′（x0）表示曲线f（x）在x=x0处的切线斜率，再代入计算．

    解答 解：y=ax-ln（x+1）的导数
    y′=2m-$\frac{1}{x+1}$，
    由在点（0，0）处的切线方程为y=3x，
    得2m-1=3，
    则m=2．
    故选：C．

    点评 本题是基础题，考查的是导数的几何意义，这个知识点在高考中是经常考查的内容，一般只要求导正确，就能够求解该题．在高考中，导数作为一个非常好的研究工具，经常会被考查到，特别是用导数研究最值，证明不等式，研究零点问题等等经常以大题的形式出现，学生在复习时要引起重视．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知函数 f （x） 对任意x∈R都有f（x）+f（1-x）=2011．
    （1）求 f（$\frac{1}{2}$）的值．
    （2）数列{an} 满足：an=f（0）+f（$\frac{1}{n}$）+f（$\frac{2}{n}$）+…+f（$\frac{n-2}{n}$）+f（$\frac{n-1}{n}$）+f（1），求数列{$\frac{{{2a}_{n}a}^{n}}{2011}$}的前n项和Sn．
    （3）若Tn=$\frac{1}{{{a}_{1}}^{2}}$+$\frac{1}{{{a}_{2}}^{2}}$+…+$\frac{1}{{{a}_{n}}^{2}}$，证明：${T_n}＜\frac{4}{{{{2011}^2}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．某公司生产某种产品投入固定资本20万元，以后生产x万件（x＞1且x∈N*）产品需再投入可变资本a（x2-1）万元，收入资金为R（x）=160x-3.8x2-1480.2万元，已知当生产10万件产品时，投入资本可达到39.8万元．
    （1）求出投入资本y（万元）关于生产产品件数x（万件）的函数解析式；
    （2）求计划生产多少万件产品时，利润最大？最大利润是多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知集合M={x|（1-x）x＞0}，N={y|y=x2+2x+3}，则（∁RM）∩N=（　　）
    A．{x|0＜x＜1}B．{x|x＞1}C．{x|x≥2}D．{x|1＜x＜2}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．直线y=m分别与曲线y=x+1，y=elogax（a＞1）交于A、B两点，当|AB|的最小值为1时，a的值为（　　）
    A．eB．2C．3D．e2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．如图是教材选修1-2中《推理与证明》一章的知识结构图，请把A处填入适当的方法综合法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．化简求值：（$\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$）÷（$\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$），其中a=2，b=-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．定义在R上的函数f（x）满足：f（x）=$\frac{{2}^{x}}{f（x-4）}$，则$\frac{f（16）}{f（0）}$=256．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

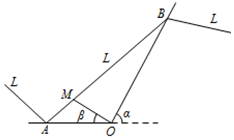    3．如图，某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB，位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km，且∠AOM=β，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，且经过大学M，其中tanα=2，cosβ=$\frac{3}{{\sqrt{13}}}$，AO=15km．
    （1）求大学M在站A的距离AM；
    （2）求铁路AB段的长AB．

    查看答案和解析>>

    同步练习册答案