
【题目】二手经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:

下面是![]() 关于
关于![]() 的折线图:
的折线图:
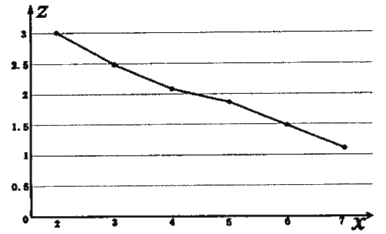
(1)由折线图可以看出,可以用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的回归方程并预测某辆
的回归方程并预测某辆![]() 型号二手汽车当使用年数为9年时售价大约为多少?(
型号二手汽车当使用年数为9年时售价大约为多少?(![]() 、
、![]() 小数点后保留两位有效数字).
小数点后保留两位有效数字).
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
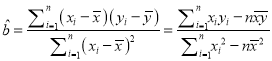 ,
,![]() .
. 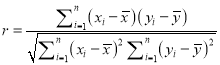 .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,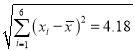 ,
,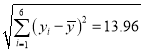 ,
,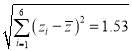 ,
,![]() ,
,![]() .
.
【答案】(1)![]() 与
与![]() 的相关系数大约为0.99,说明
的相关系数大约为0.99,说明![]() 与
与![]() 的线性相关程度很高;(2)1.46万元;
的线性相关程度很高;(2)1.46万元;
(3)11年.
【解析】
试题
(1)由已知:![]() ,
,![]() ,
, ![]() ,
, 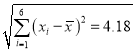 ,
,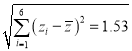 ,根据公式
,根据公式 得
得![]() .所以
.所以![]() 与
与![]() 的相关系数大约为0.99,说明
的相关系数大约为0.99,说明![]() 与
与![]() 的线性相关程度很高.(2)由公式可得,
的线性相关程度很高.(2)由公式可得,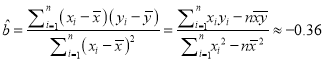 .
.![]() .可得
.可得![]() 关于
关于![]() 的回归方程为:
的回归方程为:![]() ,将
,将![]() 代入,可得
代入,可得![]() ,所以预测某辆
,所以预测某辆![]() 型号二手车当使用年数为9年时售价大约为1.46万元.(3)令
型号二手车当使用年数为9年时售价大约为1.46万元.(3)令![]() ,即
,即![]() ,所以
,所以![]() ,解不等式,即可求出结果.
,解不等式,即可求出结果.
试题解析:
(1)由已知:![]() ,
,![]() ,
,
![]() ,
, 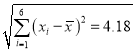 ,
,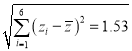 ,
,
所以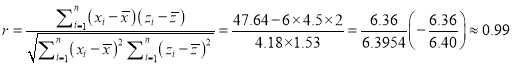 .
.
![]() 与
与![]() 的相关系数大约为0.99,说明
的相关系数大约为0.99,说明![]() 与
与![]() 的线性相关程度很高.
的线性相关程度很高.
(2)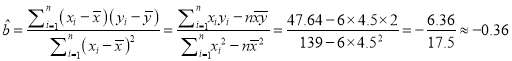 .
.
![]() .
.
所以![]() 关于
关于![]() 的线性回归直线方程为
的线性回归直线方程为![]() .
.
所以![]() 关于
关于![]() 的回归方程为:
的回归方程为:![]() ,
,
当![]() 时,
时,![]() ,
,
所以预测某辆![]() 型号二手车当使用年数为9年时售价大约为1.46万元.
型号二手车当使用年数为9年时售价大约为1.46万元.
(3)令![]() ,即
,即![]() ,
,
所以![]() ,解得:
,解得:![]() .
.
因此预测在收购该型号二手车时车辆的使用年数不得超过11年.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 是实数.
是实数.
(Ⅰ)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 为增函数,求
为增函数,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,函数![]() 有三个零点,求
有三个零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,圆
轴的正半轴,两种坐标系中的长度单位相同,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),射线
为参数),射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,且
,且![]() ,
,![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() 为坐标原点,
为坐标原点,![]() 为定值,当
为定值,当![]() 变化时,始终有
变化时,始终有![]() ,求定值
,求定值![]() 的大小;
的大小;
(3)若![]() ,
,![]() ,
,![]() ,当
,当![]() 改变时,求三角形
改变时,求三角形![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为确定下一年投入某种产品的研发费用,需了解年研发费用![]() (单位:千万元)对年销售量
(单位:千万元)对年销售量![]() (单位:千万件)的影响,统计了近10年投入的年研发费用
(单位:千万件)的影响,统计了近10年投入的年研发费用![]() 与年销售量
与年销售量![]() 的数据,得到散点图如图所示.
的数据,得到散点图如图所示.

(1)利用散点图判断![]() 和
和![]() (其中
(其中![]() 均为大于0的常数)哪一个更适合作为年销售量
均为大于0的常数)哪一个更适合作为年销售量![]() 和年研发费用
和年研发费用![]() 的回归方程类型(只要给出判断即可,不必说明理由);
的回归方程类型(只要给出判断即可,不必说明理由);
(2)对数据作出如下处理,令![]() ,得到相关统计量的值如表:根据第(1)问的判断结果及表中数据,求
,得到相关统计量的值如表:根据第(1)问的判断结果及表中数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
|
|
|
|
15 | 15 | 28.25 | 56.5 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:
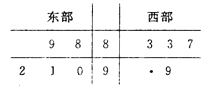
其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了![]() 位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示)
位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示)
年龄x(岁) |
|
|
|
|
周均学习成语知识时间y(小时) |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习成语知识时间.
岁观众周均学习成语知识时间.
参考公式: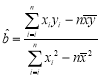 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,O为坐标原点,以O为圆心的圆与直线
中,O为坐标原点,以O为圆心的圆与直线![]() 相切.
相切.
(1)求圆O的方程.
(2)直线![]() 与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形
与圆O交于A,B两点,在圆O上是否存在一点M,使得四边形![]() 为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
为菱形?若存在,求出此时直线l的斜率;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com