解:(Ⅰ)∵f(x)=-

x
3+x
2+(m
2-1)x,(x∈R),
∴f′(x)=-x
2+2x+m
2-1.
令f′(x)=0,解得x=1-m,或x=1+m.
因为m>0,所以1+m>1-m.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,1-m) | 1-m | (1-m,1+m) | 1+m | (1+m,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ |
所以f(x)在(-∞,1-m),(1+m,+∞)内是减函数,在(1-m,1+m)内是增函数.
f(x)在x=1-m处取极小值f(1-m)=-
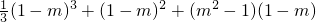
=-
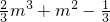
.
f(x)在x=1+m处取极大值f(1+m)=-
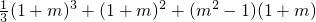
=
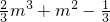
.
(Ⅱ)∵f(x)=-

x
3+x
2+(m
2-1)x,
∴g(x)=f(x)+

=-

x
3+x
2+(m
2-1)x+

,
由(Ⅰ)知:g(x)在(-∞,1-m),(1+m,+∞)内是减函数,
在(1-m,1+m)内是增函数.
在x=1-m处取极小值
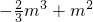
,x=1+m处取极大值
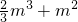
,
∵函数g(x)=f(x)+

有三个互不相同的零点,且m>0,
∴
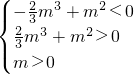
,
解得
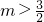
.
分析:(Ⅰ)由已知我们易求出函数的导函数,令导函数值为0,我们则求出导函数的零点,根据m>0,我们可将函数的定义域分成若干个区间,分别在每个区间上讨论导函数的符号,即可得到函数的单调区间.
(Ⅱ)根据题意求出函数的导数并且通过导数求出出原函数的单调区间,进而得到原函数的极值,因为函数存在三个不同的零点,所以结合函数的性质可得函数的极大值大于0,极小值小于0,即可单调答案.
点评:解决此类问题的关键是熟练掌握利用导数球函数的单调区间与函数的极值,并且掌握通过函数零点个数进而判断极值点与0的大小关系.

 x3+x2+(m2-1)x,(x∈R),其中m>0
x3+x2+(m2-1)x,(x∈R),其中m>0 有三个互不相同的零点,求m的取值范围.
有三个互不相同的零点,求m的取值范围. x3+x2+(m2-1)x,(x∈R),
x3+x2+(m2-1)x,(x∈R),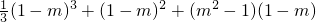 =-
=-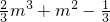 .
.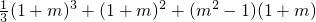 =
=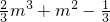 .
. x3+x2+(m2-1)x,
x3+x2+(m2-1)x, =-
=- x3+x2+(m2-1)x+
x3+x2+(m2-1)x+ ,
,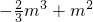 ,x=1+m处取极大值
,x=1+m处取极大值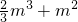 ,
, 有三个互不相同的零点,且m>0,
有三个互不相同的零点,且m>0,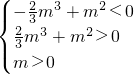 ,
,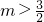 .
.

 名校课堂系列答案
名校课堂系列答案