
【题目】如图,在圆内接△ABC,A,B,C所对的边分别为a,b,c,满足acosC+ccosA=2bcosB. 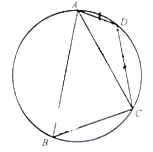
(1)求B的大小;
(2)若点D是劣弧 ![]() 上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
上一点,AB=3,BC=2,AD=1,求四边形ABCD的面积.
【答案】
(1)解:∵acosC+ccosA=2bcosB.
由正弦定理,可得sinAcosC+sinAcosA=2sinBcosB.
得sinB=2sinBcosB.
∵0<B<π,sinB≠0,
∴cosB= ![]() ,
,
即B= ![]() .
.
(2)解:在△ABC中,AB=3,BC=2,B= ![]() .
.
由余弦定理,cos ![]() =
= ![]() ,
,
可得:AC= ![]() .
.
在△ADC中,AC= ![]() ,AD=1,ABCD在圆上,
,AD=1,ABCD在圆上,
∵B= ![]() .
.
∴∠ADC= ![]() .
.
由余弦定理,cos ![]() =
= ![]() =
= ![]() .
.
解得:DC=2
四边形ABCD的面积S=S△ABC+S△ADC= ![]() ADDCsin
ADDCsin ![]() +
+ ![]() ABBCsin
ABBCsin ![]() =2
=2 ![]() .
.
【解析】(1)根据正弦定理化简即可.(2)在△ABC,利用余弦定理求出AC,已知B,可得∠ADC,再余弦定理求出DC,即可△ABC和△ADC面积,可得四边形ABCD的面积.


科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为 . 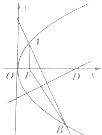
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的等差数列{an}前n项和为Sn , 首项a1=3,数列{bn} 为等比数列,首项b1=1,且b2S2=64,b3S3=960.
(1)求an和bn;
(2)设f(n)= ![]() (n∈N*),求f(n)最大值及相应的n的值.
(n∈N*),求f(n)最大值及相应的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1 , a2 , a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{ ![]() }为等差数列,求实数t;
}为等差数列,求实数t;
(3)构造数列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,若该数列前n项和Tn=1821,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在同时满足下列两条件的直线l:l与抛物线y2=8x有两个不同的交点A和B;线段AB被直线l1:x+5y﹣5=0垂直平分.若不存在,说明理由,若存在,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 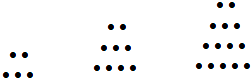
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准03.5,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图.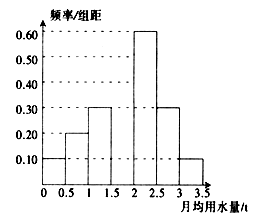
(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准03.5,则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com