
°ĺŐ‚ńŅ°Ņ°įłÓ‘≤ ű°Ī «ŃűĽ’◊ÓÕĽ≥ŲĶń ż—ß≥…ĺÕ÷ģ“Ľ£¨ňŻ‘ŕ°∂ĺŇ’¬ň„ ű◊Ę°∑÷–ŐŠ≥ŲłÓ‘≤ ű£¨≤Ę◊ųő™ľ∆ň„‘≤Ķń÷‹≥§£¨√śĽż“—ĺ≠‘≤÷‹¬ ĶńĽýī°£¨ŃűĽ’į—‘≤ńŕĹ”’ż∂ŗĪŖ–őĶń√śĽż“Ľ÷Īň„ĶĹŃň’ż3072ĪŖ–ő£¨≤Ę”…īň∂Ý«ůĶ√Ńň‘≤÷‹¬ ő™3.1415ļÕ3.1416’‚ŃĹłŲĹŁň∆ ż÷Ķ£¨’‚łŲĹŠĻŻ «ĶĪ Ī ņĹÁ…Ō‘≤÷‹¬ ľ∆ň„Ķń◊Óĺę»∑ żĺ›.»ÁÕľ£¨ĶĪ∑÷łÓĶĹ‘≤ńŕĹ”’żŃýĪŖ–ő Ī£¨ń≥Õ¨—ßņŻ”√ľ∆ň„ĽķňśĽķń£ń‚∑®ŌÚ‘≤ńŕňśĽķÕ∂÷ņĶ„£¨ľ∆ň„Ķ√≥Ųł√Ķ„¬š‘ŕ’żŃýĪŖ–őńŕĶń∆Ķ¬ ő™0.8269£¨ń«√īÕ®Ļżł√ Ķ—ťľ∆ň„≥ŲņīĶń‘≤÷‹¬ ĹŁň∆÷Ķő™£®≤őŅľ żĺ›£ļ![]() £©
£©

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
 Ķ„嶖¬ĹŐ≤ń»ęń‹Ĺ‚∂ŃŌĶŃ–īūįł
Ķ„嶖¬ĹŐ≤ń»ęń‹Ĺ‚∂ŃŌĶŃ–īūįł –°—ßĹŐ≤ńÕÍ»ęĹ‚∂ŃŌĶŃ–īūįł
–°—ßĹŐ≤ńÕÍ»ęĹ‚∂ŃŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™ŃňŃňĹ‚–°—ß…ķĶńŐŚń‹«ťŅŲ£¨≥ť»°Ńňń≥–°—ßÕ¨ńÍľ∂≤Ņ∑÷—ß…ķĹÝ––ŐÝ…Ģ≤‚ ‘£¨ĹęňýĶ√Ķń żĺ›’ŻņŪļůĽ≠≥Ų∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨“—÷™Õľ÷–ī”◊ůĶĹ”“Ķń«į»żłŲ–°◊ťĶń∆Ķ¬ ∑÷Īū «0.1£¨0.3£¨0.4Ķŕ“Ľ–°◊ťĶń∆Ķ ż «5.
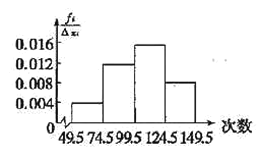
£®1£©«ůĶŕňń–°◊ťĶń∆Ķ¬ ļÕł√◊ť≤őľ”’‚īő≤‚ ‘Ķń—ß…ķ»ň ż£Ľ
£®2£©‘ŕ’‚īő≤‚ ‘÷–£¨—ß…ķŐÝ…Ģīő żĶń÷–őĽ–߬š‘ŕĶŕľł–°◊ťńŕ£Ņ
£®3£©ī”Ķŕ“Ľ–°◊ť÷–—°≥Ų2»ň£¨Ķ໿–°◊ť÷–—°≥Ų3»ň◊ť≥…∂”őťīķĪŪ—ß–£≤őľ”«ÝņÔĶń–°—ß…ķŐŚ÷ ≤‚ ‘£¨‘ŕ≤‚ ‘Ķńń≥“ĽĽ∑Ĺŕ£¨–Ť“™ī”’‚5»ň÷–»ő—°ŃĹ»ň≤őľ”≤‚ ‘£¨«ů’‚ŃĹ»ňņī◊‘Õ¨“Ľ–°◊ťĶńłŇ¬ .
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńņ‚◊∂![]() ÷–£¨Ķ◊√ś
÷–£¨Ķ◊√ś![]() ő™Ő›–ő£¨
ő™Ő›–ő£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨
£¨![]() ∑÷Īū «
∑÷Īū «![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.
£®ĘŮ£©«ů÷§£ļ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®ĘÚ£©»Ű![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…ĶńĹ«ő™
ňý≥…ĶńĹ«ő™![]() £¨«ůŌŖ∂ő
£¨«ůŌŖ∂ő![]() Ķń≥§.
Ķń≥§.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ÷Īňńņ‚÷ý![]() ÷–£¨Ķ◊√ś
÷–£¨Ķ◊√ś![]() «ĺō–ő£¨
«ĺō–ő£¨![]() ”Ž
”Ž![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨
£¨![]() .
.
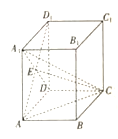
£®1£©÷§√ų£ļ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®2£©«ů÷ĪŌŖ![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ňńņ‚◊∂![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨PA=PD=CD=BC=1.
£¨PA=PD=CD=BC=1.
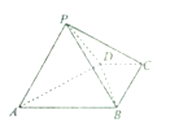
£®1£©«ů÷§£ļ∆Ĺ√ś![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®2£©«ů÷ĪŌŖ![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
ňý≥…Ĺ«Ķń’żŌ“÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…ŤP «Õ÷‘≤![]() …Ō“ĽĶ„£¨M£¨N∑÷Īū «ŃĹ‘≤(x£ę4)2£ęy2£Ĺ1ļÕ(x£≠4)2£ęy2£Ĺ1…ŌĶńĶ„£¨‘Ú|PM|£ę|PN|Ķń◊Ó–°÷Ķ°Ę◊Óīů÷Ķ∑÷Īūő™ £® £©
…Ō“ĽĶ„£¨M£¨N∑÷Īū «ŃĹ‘≤(x£ę4)2£ęy2£Ĺ1ļÕ(x£≠4)2£ęy2£Ĺ1…ŌĶńĶ„£¨‘Ú|PM|£ę|PN|Ķń◊Ó–°÷Ķ°Ę◊Óīů÷Ķ∑÷Īūő™ £® £©
A. 9,12 B. 8,11 C. 10,12 D. 8,12
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ ÷Ľķ≥ß…ŐÕ∆≥Ų“ĽŅÓ6īÁīů∆Ń ÷Ľķ£¨Ō÷∂‘500√Żł√ ÷Ľķ Ļ”√’Ŗ£®200√ŻŇģ–‘£¨300√Żń––‘£©ĹÝ––Ķų≤ť£¨∂‘ ÷ĽķĹÝ––∆ņ∑÷£¨∆ņ∑÷Ķń∆Ķ ż∑÷≤ľĪŪ»ÁŌ¬£ļ
Ňģ–‘”√Ľß | ∑÷÷Ķ«Ýľš | [50£¨60£© | [60£¨70£© | [70£¨80£© | [80£¨90£© | [90£¨100] |
∆Ķ ż | 20 | 40 | 80 | 50 | 10 | |
ń––‘”√Ľß | ∑÷÷Ķ«Ýľš | [50£¨60£© | [60£¨70£© | [70£¨80£© | [80£¨90£© | [90£¨100] |
∆Ķ ż | 45 | 75 | 90 | 60 | 30 |
£®1£©ÕÍ≥…Ō¬Ń–∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£¨≤ĘĪ»ĹŌŇģ–‘”√ĽßļÕń––‘”√Ľß∆ņ∑÷Ķń≤®∂Įīů–°£®≤Ľľ∆ň„ĺŖŐŚ÷Ķ£¨łÝ≥ŲĹŠ¬ŘľīŅ…£©£Ľ

£®2£©į—∆ņ∑÷≤ĽĶÕ”ŕ70∑÷Ķń”√Ľß≥∆ő™°į∆ņ∑÷Ńľļ√”√Ľß°Ī£¨ń‹∑Ů”–![]() Ķńį—ő’»Ōő™°į∆ņ∑÷Ńľļ√”√Ľß°Ī”Ž–‘Īū”–Ļō£Ņ
Ķńį—ő’»Ōő™°į∆ņ∑÷Ńľļ√”√Ľß°Ī”Ž–‘Īū”–Ļō£Ņ
≤őŅľłĹĪŪ£ļ
|
|
|
| |
|
|
|
|
|
≤őŅľĻę Ĺ £¨∆š÷–
£¨∆š÷–![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ żf£®x£©£Ĺax2©Ābx+lnx£¨£®a£¨b° R£©£ģ
£®1£©»Űa£Ĺ1£¨b£Ĺ3£¨«ůļĮ żf£®x£©ĶńĶ•Ķų‘Ų«Ýľš£Ľ
£®2£©»Űb£Ĺ0 Ī£¨≤ĽĶ» Ĺf£®x£©°‹0‘ŕ[1£¨+°ř£©…Ōļ„≥…ŃĘ£¨«ů Ķ żaĶń»°÷Ķ∑∂őߣĽ
£®3£©ĶĪa£Ĺ1£¨b£ĺ![]() Ī£¨ľ«ļĮ żf£®x£©ĶńĶľļĮ żf
Ī£¨ľ«ļĮ żf£®x£©ĶńĶľļĮ żf![]() £®x£©ĶńŃĹłŲŃ„Ķ„ «x1ļÕx2£®x1£ľx2£©£¨«ů÷§£ļf£®x1£©©Āf£®x2£©£ĺ
£®x£©ĶńŃĹłŲŃ„Ķ„ «x1ļÕx2£®x1£ľx2£©£¨«ů÷§£ļf£®x1£©©Āf£®x2£©£ĺ![]() ©Ā3ln2£ģ
©Ā3ln2£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕĹĽÕ®Ļ§≥Ő—ß÷–£¨≥£◊ų»ÁŌ¬∂®“Ś£ļĹĽÕ®ŃųŃŅ![]() £®Ńĺ/–° Ī£©£ļĶ•őĽ ĪľšńŕÕ®ĻżĶņ¬∑…Ōń≥“ĽļŠ∂Ō√śĶń≥ĶŃĺ ż£Ľ≥ĶŃųňŔ∂»
£®Ńĺ/–° Ī£©£ļĶ•őĽ ĪľšńŕÕ®ĻżĶņ¬∑…Ōń≥“ĽļŠ∂Ō√śĶń≥ĶŃĺ ż£Ľ≥ĶŃųňŔ∂»![]() £®«ß√◊/–° Ī£©£ļĶ•őĽ Īľšńŕ≥ĶŃų∆Ĺĺý–– ĽĻżĶńĺŗņŽ£Ľ≥ĶŃų√‹∂»
£®«ß√◊/–° Ī£©£ļĶ•őĽ Īľšńŕ≥ĶŃų∆Ĺĺý–– ĽĻżĶńĺŗņŽ£Ľ≥ĶŃų√‹∂»![]() £®Ńĺ/«ß√◊£©£ļĶ•őĽ≥§∂»Ķņ¬∑…Ōń≥“Ľň≤ľšňýīś‘ŕĶń≥ĶŃĺ ż. “Ľį„Ķń£¨
£®Ńĺ/«ß√◊£©£ļĶ•őĽ≥§∂»Ķņ¬∑…Ōń≥“Ľň≤ľšňýīś‘ŕĶń≥ĶŃĺ ż. “Ľį„Ķń£¨![]() ļÕ
ļÕ![]() ¬ķ◊„“ĽłŲŌŖ–‘ĻōŌĶ£¨ľī
¬ķ◊„“ĽłŲŌŖ–‘ĻōŌĶ£¨ľī![]() £®∆š÷–
£®∆š÷–![]() «’ż ż£©£¨‘Ú“‘Ō¬ňĶ∑®’ż»∑Ķń «
«’ż ż£©£¨‘Ú“‘Ō¬ňĶ∑®’ż»∑Ķń «
A. ňś◊Ň≥ĶŃų√‹∂»‘Ųīů£¨≥ĶŃųňŔ∂»‘Ųīů
B. ňś◊Ň≥ĶŃų√‹∂»‘Ųīů£¨ĹĽÕ®ŃųŃŅ‘Ųīů
C. ňś◊Ň≥ĶŃų√‹∂»‘Ųīů£¨ĹĽÕ®ŃųŃŅŌ»ľű–°£¨ļů‘Ųīů
D. ňś◊Ň≥ĶŃų√‹∂»‘Ųīů£¨ĹĽÕ®ŃųŃŅŌ»‘Ųīů£¨ļůľű–°
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com