
【题目】如图,点![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点, ![]() 的长轴是圆
的长轴是圆![]() 的直径.
的直径. ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于两点
于两点![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积取最大值时直线
面积取最大值时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题意可得b=1,2a=4,即可得到椭圆的方程;(2)设A(x1,y1),B(x2,y2),D(x0,y0).由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx﹣1.利用点到直线的距离公式和弦长公式即可得出圆心O到直线l1的距离和弦长|AB|,又l2⊥l1,可得直线l2的方程为x+kx+k=0,与椭圆的方程联立即可得到点D的横坐标,即可得出|PD|,即可得到三角形ABD的面积,利用基本不等式的性质即可得出其最大值,即得到k的值.
(1)由已知得到![]() ,且
,且![]() ,所以椭圆的方程是
,所以椭圆的方程是![]() ;
;
(2)因为直线![]() ,且都过点
,且都过点![]() ,所以
,所以
①当直线![]() 的斜率不存在时,易知直线与
的斜率不存在时,易知直线与![]() 椭圆
椭圆![]() 相切,不合题意.
相切,不合题意.
②当直线![]() 的斜率存在且不为
的斜率存在且不为![]() 时,设直线
时,设直线![]() ,
,
直线![]() ,所以圆心
,所以圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以直线
,所以直线![]() 被圆
被圆![]() 所截的弦
所截的弦 ;
;
由 ,所以
,所以 ,所以
,所以
 ,
,
(当 时,等号成立.)
时,等号成立.)
③当![]() 时,
时, ![]() .
.
综上所述,当![]() 面积取最大值时直线
面积取最大值时直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且an和Sn满足:4Sn=(an+1)2(n=1,2,3…),
(1)求{an}的通项公式;
(2)设bn= ![]() ,求{bn}的前n项和Tn .
,求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个分类变量X和Y,值域分别为{x1,x2}和{y1,y2},其样本频数分别是a=10,b=21,c+d=35.若X与Y有关系的可信程度不小于97.5%,则c等于( )
A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有两个命题:p:关于x的不等式x2+2x-4-a≥0对一切x∈R恒成立;q:已知a≠0,a≠±1,函数y=-|a|x在R上是减函数,若p∧q为假命题,p∨q为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列各命题作为原命题,分别写出它们的逆命题、否命题和逆否命题.
(1)若α=β,则sin α=sin β;
(2)若对角线相等,则梯形为等腰梯形;
(3)已知a,b,c,d都是实数,若a=b,c=d,则a+c=b+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() (含端点)上运动,当点
(含端点)上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
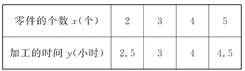
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com