
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
【答案】(1){x|x≤-1或x=1};(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)把![]() 代入函数解析式,分段后分段求解方程
代入函数解析式,分段后分段求解方程![]() 的解集,取并集后得答案;(2)分段写出函数
的解集,取并集后得答案;(2)分段写出函数![]() 的解析式,由
的解析式,由![]() 在
在![]() 上单调递增,则需第一段二次函数的对称轴小于等于
上单调递增,则需第一段二次函数的对称轴小于等于![]() ,第二段一次函数的一次项系数大于0,且第二段函数的最大值小于等于第一段函数的最小值,联立不等式组后求解
,第二段一次函数的一次项系数大于0,且第二段函数的最大值小于等于第一段函数的最小值,联立不等式组后求解![]() 的取值范围;(3)把不等式
的取值范围;(3)把不等式![]() 对一切实数
对一切实数![]() 恒成立转化为函数
恒成立转化为函数![]() 对一切实数
对一切实数![]() 恒成立,然后对
恒成立,然后对![]() 进行分类讨论,利用函数单调性求得
进行分类讨论,利用函数单调性求得![]() 的范围,取并集后得答案.
的范围,取并集后得答案.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ;当
;当![]() 时,由
时,由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ;当
;当![]() 时,
时, ![]() 恒成立,∴方程的解集为
恒成立,∴方程的解集为![]() 或
或![]() .
.
(2)由题意知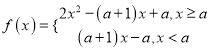 ,若
,若![]() 在R上单调递增,则
在R上单调递增,则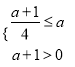 解得
解得![]() ,∴实数
,∴实数![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() ,则
,则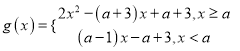 ,不等式
,不等式![]() 对任意
对任意![]() 恒成立,等价于不等式
恒成立,等价于不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
①若![]() ,则
,则![]() ,即
,即![]() ,取
,取![]() ,此时
,此时![]() ,∴
,∴![]() ,即对任意的
,即对任意的![]() ,总能找到
,总能找到![]() ,使得
,使得![]() ,∴不存在
,∴不存在![]() ,使得
,使得![]() 恒成立.
恒成立.
②若![]() ,则
,则![]() ,∴
,∴![]() 的值域为
的值域为![]() ,∴
,∴![]() 恒成立③若
恒成立③若![]() ,当
,当![]() 时,
时, ![]() 单调递减,其值域为
单调递减,其值域为![]() ,由于
,由于![]() ,所以
,所以![]() 恒成立,当
恒成立,当![]() 时,由
时,由![]() ,知
,知![]() ,
, ![]() 在
在![]() 处取得最小值,令
处取得最小值,令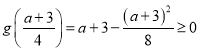 ,得
,得![]() ,又
,又![]() ,∴
,∴![]() ,综上,
,综上, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=emx+x2-mx.
(1)证明:f(x)在(-∞,0)单调递减,在(0,+∞)单调递增;
(2)若对于任意x1,x2∈[-1,1],都有![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856312)[选修4-5:不等式选讲]
已知函数f(x)=|x-m|-2|x-1|(m∈R).
(Ⅰ)当m=3时,求函数f(x)的最大值;
(Ⅱ)解关于x的不等式f(x)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
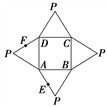
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
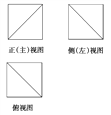
【题目】如图,已知正方体ABCD-A′B′C′D′的外接球的体积为![]() π,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
π,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
A. ![]() +
+![]() B. 3+
B. 3+![]() 或
或![]() +
+![]() C. 3+
C. 3+![]() D.
D. ![]() +
+![]() 或2+
或2+![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃![]() ,梅花
,梅花![]() ,方片
,方片![]() 以及黑桃
以及黑桃![]() ,让明、小红、小张、小李四个人进行猜测:
,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
小红说:第2个盒子里面饭的是梅花![]() ,第3个盒子里放的是黑桃
,第3个盒子里放的是黑桃![]() ;
;
小张说:第4个盒子里面放的是黑桃![]() ,第2个盒子里面放的是方片
,第2个盒子里面放的是方片![]() ;
;
小李说:第4个盒子里面放的是红桃![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃![]() 或黑桃
或黑桃![]() B. 红桃
B. 红桃![]() 或梅花
或梅花![]()
C. 黑桃![]() 或方片
或方片![]() D. 黑桃
D. 黑桃![]() 或梅花
或梅花![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,
f(x)=![]() .
.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com