
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
分析 根据条件判断函数f(x)是周期函数,利用函数的周期性进行求解即可.
解答 解:取x=1,y=0得$f(0)=\frac{1}{2}$
法一:根据已知知$f(1)=\frac{1}{4}$
取x=1,y=1得f(2)=-$\frac{1}{4}$
取x=2,y=1得f(3)=-$\frac{1}{2}$
取x=2,y=2得f(4)=-$\frac{1}{4}$
取x=3,y=2得f(5)=$\frac{1}{4}$
取x=3,y=3得f(6)=$\frac{1}{2}$
猜想得周期为6;
法二:取x=1,y=0得$f(0)=\frac{1}{2}$
取x=n,y=1,有f(n)=f(n+1)+f(n-1),
同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)=-f(n-1)
所以f(n)=-f(n+3)=f(n+6)
所以函数是周期函数,周期T=6,
故f(2017)=f(336×6+1)=f(1)=$\frac{1}{4}$,
故选:A.
点评 本题主要考查函数值的计算,准确找出周期是此类问题(项数很大)的关键,分别可以用归纳法和演绎法得出周期,解题时根据自己熟悉的方法得出即可.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}}]$ | B. | $[{-\frac{1}{2},+∞})$ | C. | $[{-\frac{1}{2},0})$ | D. | $[-\frac{1}{2},0]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,2 | B. | -1,-2 | C. | 1,$\frac{1}{2}$ | D. | -1,-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
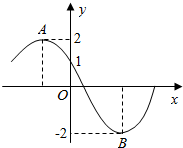 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com