
思路解析:设P点的坐标,列方程组解得坐标.
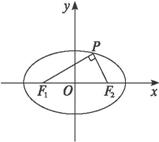
解法一:设P(x0,y0)(x0>0,y0>0),椭圆的两焦点分别是F1(-5,0)、F2(5,0),如图所示,则![]() ·
·![]() =-1.
=-1.
∴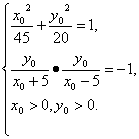
解方程组,得x0=3,y0=4.
∴P(3,4).
解法二:设P(x0,y0)(x0>0,y0>0),
则有a=3![]() ,b=2
,b=2![]() ,∴c=5,e=
,∴c=5,e=![]() .
.
∴|PF1|=a+ex0=3![]() +
+![]() x0,|PF2|=a-ex0=3
x0,|PF2|=a-ex0=3![]() -
-![]() x0,|F1F2|=2c=10.
x0,|F1F2|=2c=10.
∵PF1⊥PF2,∴|PF1|2+|PF2|2=|F1F2|2.
∴(3![]() +
+![]() x0)2+(3
x0)2+(3![]() -
-![]() x0)2=100.
x0)2=100.
解得x0=±3.
∵x0>0,y0>0,∴x0=3,y0=4.∴P(3,4).
方法归纳
当已知两直线互相垂直时,常想到其斜率之积为-1;当已知椭圆上一点P时,常想到点P的坐标是椭圆方程的一组解.椭圆上的点与焦点连线,常联想焦半径公式.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
| |OP| | |OM| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 9 |
| AP |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 9 |
| AM |
| BM |
查看答案和解析>>
科目:高中数学 来源: 题型:
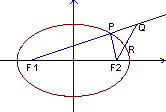
已知椭圆![]() =1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线
=1,点P为其上一点,F1、F2为椭圆的焦点,Q为射线![]() 延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
延长线上一点,且|PQ|=|PF2|,设R为F2Q的中点。
(1)当P点在椭圆上运动时,求R形成的轨迹方程;
(2)设点R形成的曲线为C,直线l:y=k(x+4![]() )与曲线C相交于A、B两点,若∠AOB=90o时,
)与曲线C相交于A、B两点,若∠AOB=90o时,
求k的值.
(请注意把答案填写在答题卡上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com