B
分析:由函数f(x)=(a-3)x-ax
3在区间[-1,1]上的最小值等于-3,由函数解析式先求其导函数,进而可判断函数在区间[-1,1]上的单调性,从而可求函数的最小值,即可
解答:由函数f(x)=(a-3)x-ax
3 求导函数为:f
′(x)=-3ax
2+(a-3),
①当a=0时,f(x)=-3x,此时函数在定义域内单调递减,所以函数的最小值为:f(1)=-3,符合题意,
所以a=0符合题意;
②当a≠0时,f
‘(x)=0,即 3ax
2=a-3
(I)当0<a≤3时,f
′(x)=-3ax
2+(a-3)为开口向下的二次函数,且△=12a(a-3)≤0,f
‘(x)≤0恒成立
所以函数f(x)在定义域上为单调递减函数,函数的最小值为f(1)=-3,此时符合题意;
(II)当a<0或a>3时,f
′(x)=0,即 3ax
2=a-3
解得:
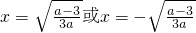
,
①当
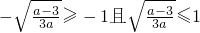
,即a
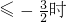
,
函数f(x)在[-1,-
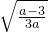
]上单调递增,在
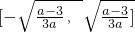
上单调递减,在
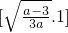
上单调递增,
所以此时函数在定义域的最小值为f(-1)=-3或f(-
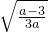
)=
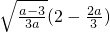
令
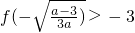
解得:a∈φ
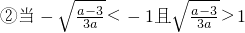
,
即
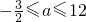
时,函数在定义域上始终单调递减,则函数在定义域上的最小值为f(1)=-3,符合题意.
综上所述:当即

时符合题意.
故选B
点评:此题考查了利用导数求函数的单调区间,还考查了学生在函数字母的不等式分类讨论思想及学生的计算能力.

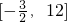
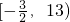
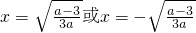 ,
,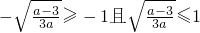 ,即a
,即a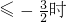 ,
,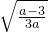 ]上单调递增,在
]上单调递增,在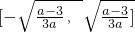 上单调递减,在
上单调递减,在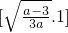 上单调递增,
上单调递增,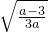 )=
)=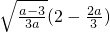 令
令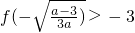
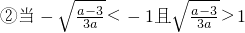 ,
,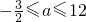 时,函数在定义域上始终单调递减,则函数在定义域上的最小值为f(1)=-3,符合题意.
时,函数在定义域上始终单调递减,则函数在定义域上的最小值为f(1)=-3,符合题意. 时符合题意.
时符合题意.

 天天向上口算本系列答案
天天向上口算本系列答案