
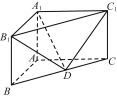
【题目】在直三棱柱ABC-A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点.
(1) 求直线DC1与平面A1B1D所成角的正弦值;
(2) 求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)以![]() 为正交基底,建立如图所示的空间直角坐标系,求得平面A1B1D的法向量的一个法向量,利用向量的夹角公式,即可求解;
为正交基底,建立如图所示的空间直角坐标系,求得平面A1B1D的法向量的一个法向量,利用向量的夹角公式,即可求解;
(2) 由(1)知![]() =(-1,2,3),
=(-1,2,3),![]() =(-2,4,0),求得平面B1DC1的法向量,利用下向量的夹角公式,即可求解.
=(-2,4,0),求得平面B1DC1的法向量,利用下向量的夹角公式,即可求解.
(1) 在直三棱柱![]() 中,有AB⊥AC,AA1⊥AB,AA1⊥AC,
中,有AB⊥AC,AA1⊥AB,AA1⊥AC,
故可以![]() 为正交基底,建立如图所示的空间直角坐标系.
为正交基底,建立如图所示的空间直角坐标系.
因为AB=2,AC=4,AA1=3,
所以A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3).
因为D是BC的中点,所以D(1,2,0),所以![]() .
.
设![]() (x1,y1,z1)为平面A1B1D的法向量,
(x1,y1,z1)为平面A1B1D的法向量,
因为![]() ,
,
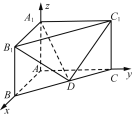
所以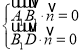 ,即
,即 ,
,
令y1=3,则x1=0,z1=2,所以平面A1B1D的一个法向量为![]() (0,3,2).
(0,3,2).
设直线DC1与平面A1B1D所成的角为θ,
则![]() ,
,
所以直线DC1与平面A1B1D所成角的正弦值为![]() .
.
(2) 由(1)知![]() =(-1,2,3),
=(-1,2,3),![]() =(-2,4,0),
=(-2,4,0),
设![]() =(x2,y2,z2)为平面B1DC1的法向量,则
=(x2,y2,z2)为平面B1DC1的法向量,则 ,即
,即 ,
,
令x2=2,则y2=1,z2=0,所以平面B1DC1的一个法向量为![]() =(2,1,0).
=(2,1,0).
同理可以求得平面A1DC1的一个法向量n3=(3,0,1),
所以![]() ,
,
由图可知二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题甲是命题乙的充分非必要条件,命题丙是命题乙的必要非充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( )
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设函数![]() 的极值点为
的极值点为![]() ,当
,当![]() 变化时,点(
变化时,点(![]() ,
,![]() )构成曲线M.证明:任意过原点的直线
)构成曲线M.证明:任意过原点的直线![]() ,与曲线M均仅有一个公共点.
,与曲线M均仅有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
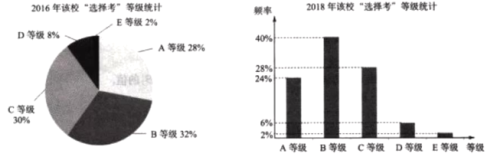
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图判断闰年的流程图,判断公元1900年、公元2000年、公元2018年、公元2020年这四年中闰年的个数为(nMODm为n除以m的余数)( )
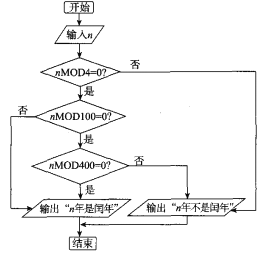
A.1个B.2个
C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com