Question

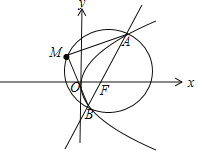
【题目】已知过抛物线C：y2＝8x的焦点且斜率为k的直线与C交于A、B两点，若以AB为直径的圆过点M（﹣2，2），则k＝（　　）

A.B.C.D.2

Answer 1

【答案】D

【解析】

写出直线的点斜式方程，与抛物线方程联立得出A，B两点的坐标关系，根据kAMkBM＝﹣1列方程解出k

解：抛物线y2＝8x的焦点F（2，0），设直线AB的方程为y＝k（x﹣2），

联立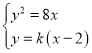，得k2x﹣（4k2+8）x+4k2＝0．

设A（x1，y1），B（x2，y2），

则x1+x2＝4，x1x2＝4．

∴y1+y2＝k（x1+x2）﹣4k，y1y2＝﹣16．

∵以AB为直径的圆过点M（﹣2，2），∴kAMkBM＝﹣1，

即1．

∴y1y2﹣2（y1+y2）+4+x1x2+2（x1+x2）+4＝0．

∴﹣164+4+2（4）+4＝0，

整理得：k2﹣4k+4＝0，解得k＝2．

故选：D．