
【题目】已知函数f0(x)= ![]() (x>0),设fn(x)为fn﹣1(x)的导数,n∈N* .
(x>0),设fn(x)为fn﹣1(x)的导数,n∈N* .
(1)求2f1( ![]() )+
)+ ![]() f2(
f2( ![]() )的值;
)的值;
(2)证明:对任意n∈N* , 等式|nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )|=
)|= ![]() 都成立.
都成立.
【答案】
(1)解:∵f0(x)= ![]() ,∴xf0(x)=sinx,
,∴xf0(x)=sinx,
则两边求导,[xf0(x)]′=(sinx)′,
∵fn(x)为fn﹣1(x)的导数,n∈N*,
∴f0(x)+xf1(x)=cosx,
两边再同时求导得,2f1(x)+xf2(x)=﹣sinx,
将x= ![]() 代入上式得,2f1(
代入上式得,2f1( ![]() )+
)+ ![]() f2(
f2( ![]() )=﹣1
)=﹣1
(2)证明:由(1)得,f0(x)+xf1(x)=cosx=sin(x+ ![]() ),
),
恒成立两边再同时求导得,2f1(x)+xf2(x)=﹣sinx=sin(x+π),
再对上式两边同时求导得,3f2(x)+xf3(x)=﹣cosx=sin(x+ ![]() ),
),
同理可得,两边再同时求导得,4f3(x)+xf4(x)=sinx=sin(x+2π),
猜想得,nfn﹣1(x)+xfn(x)=sin(x+ ![]() )对任意n∈N*恒成立,
)对任意n∈N*恒成立,
下面用数学归纳法进行证明等式成立:
①当n=1时, ![]() 成立,则上式成立;
成立,则上式成立;
②假设n=k(k>1且k∈N*)时等式成立,即 ![]() ,
,
∵[kfk﹣1(x)+xfk(x)]′=kfk﹣1′(x)+fk(x)+xfk′(x)
=(k+1)fk(x)+xfk+1(x)
又 ![]()
= ![]() =
= ![]() =
= ![]() ,
,
∴那么n=k+1(k>1且k∈N*)时.等式 ![]() 也成立,
也成立,
由①②得,nfn﹣1(x)+xfn(x)=sin(x+ ![]() )对任意n∈N*恒成立,
)对任意n∈N*恒成立,
令x= ![]() 代入上式得,nfn﹣1(
代入上式得,nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )=sin(
)=sin( ![]() +
+ ![]() )=±cos
)=±cos ![]() =±
=± ![]() ,
,
所以,对任意n∈N*,等式|nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )|=
)|= ![]() 都成立
都成立
【解析】(1)由于求两个函数的相除的导数比较麻烦,根据条件和结论先将原函数化为:xf0(x)=sinx,然后两边求导后根据条件两边再求导得:2f1(x)+xf2(x)=﹣sinx,把x= ![]() 代入式子求值;(2)由(1)得,f0(x)+xf1(x)=cosx和2f1(x)+xf2(x)=﹣sinx,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后再把x=
代入式子求值;(2)由(1)得,f0(x)+xf1(x)=cosx和2f1(x)+xf2(x)=﹣sinx,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后再把x= ![]() 代入所给的式子求解验证.
代入所给的式子求解验证.
【考点精析】本题主要考查了基本求导法则的相关知识点,需要掌握若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】将函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材上一例问题如下:
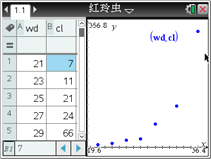
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时,先作出散点图(如图所示),发现两个变量不呈线性相关关系. 根据已有的函数知识,发现样本点分布在某一条指数型曲线![]() 的附近(
的附近(![]() 和
和![]() 是待定的参数),于是进行了如下的计算:
是待定的参数),于是进行了如下的计算:
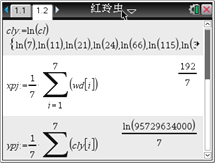
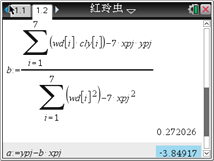
根据以上计算结果,可以得到红铃虫的产卵数y对温度x的回归方程为__________.(精确到0.0001) (提示:![]() 利用代换可转化为线性关系)
利用代换可转化为线性关系)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润![]() (元)与年产量
(元)与年产量![]() (吨)满足函数关系
(吨)满足函数关系![]() .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方![]() 元(以下称
元(以下称![]() 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量![]() (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额![]() (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格![]() 是多少?
是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e﹣x , 其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,试比较ea﹣1与ae﹣1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公路AM,AN围成一块顶角为α的角形耕地,其中tanα=-2,在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,![]() km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
km,现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园,为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的所有棱长都相等,AC∩BD=O, 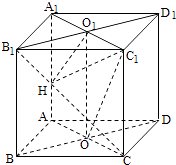 A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
A1C1∩B1D1=O1 , 四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1﹣OB1﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)满足 ![]() f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
①f(x)=sin ![]() x,g(x)=cos
x,g(x)=cos ![]() x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则实数a的取值范围是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,﹣1)
D.(﹣∞,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com