
分析 (1)当点M为椭圆的短轴的一个端点时,不妨设为(0,1),可得S△OAM=$\frac{1}{2}$c.当点M不为椭圆的短轴的一个端点时,设直线OM的方程为:y=kx,与椭圆方程联立,解得x2,y2,可得|OM|=$\sqrt{{x}^{2}+{y}^{2}}$.直线AB的方程为:y=k(x+c),点O到直线AB的距离d=$\frac{|kc|}{\sqrt{1+{k}^{2}}}$.利用S△OAM=$\frac{1}{2}d|AB|$,即可得出.
(2)证明:当点M为椭圆的短轴的一个端点时,不妨设为(0,1),可得AB⊥x轴,|FA|=|FB|=$\frac{{b}^{2}}{a}$=$\frac{1}{a}$,即可证明|FA|•|FB|=$\frac{|OM{|}^{2}}{{a}^{2}}$.当点M不为椭圆的短轴的一个端点时,设直线OM的方程为:y=kx,与椭圆方程联立解得x2,y2,可得|OM|2=x2+y2=$\frac{{a}^{2}(1+{k}^{2})}{1+{k}^{2}{a}^{2}}$.直线AB的方程为:y=k(x+c),与椭圆方程联立化为:(1+a2k2)x2+2a2k2cx+a2c2k2-a2=0,利用根与系数的关系可得:|FA|•|FB|=(ex1+a)(ex2+a)=e2x1x2+ae(x1+x2)+a2=$\frac{{k}^{2}+1}{1+{a}^{2}{k}^{2}}$,(a2-c2=1).即可证明.
解答 (1)解:当点M为椭圆的短轴的一个端点时,不妨设为(0,1),∵AB∥OM,则AB⊥x轴,∴S△OAM=$\frac{1}{2}bc$=$\frac{1}{2}$c.
当点M不为椭圆的短轴的一个端点时,设直线OM的方程为:y=kx,联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{a}^{2}{y}^{2}={a}^{2}}\end{array}\right.$,解得x2=$\frac{{a}^{2}}{1+{k}^{2}{a}^{2}}$,y2=$\frac{{k}^{2}{a}^{2}}{1+{k}^{2}{a}^{2}}$,
∴|OM|=$\sqrt{{x}^{2}+{y}^{2}}$=$a\sqrt{\frac{1+{k}^{2}}{1+{k}^{2}{a}^{2}}}$.
直线AB的方程为:y=k(x+c),点O到直线AB的距离d=$\frac{|kc|}{\sqrt{1+{k}^{2}}}$.
∴S△OAM=$\frac{1}{2}d|AB|$=$\frac{1}{2}$•$\frac{|kc|}{\sqrt{1+{k}^{2}}}$•$a\sqrt{\frac{1+{k}^{2}}{1+{k}^{2}{a}^{2}}}$=$\frac{1}{2}•\frac{ca|k|}{\sqrt{1+{k}^{2}{a}^{2}}}$=$\frac{1}{2}c$$•\frac{1}{\sqrt{\frac{1}{{k}^{2}{a}^{2}}+1}}$$<\frac{1}{2}c$.
因此当AB⊥x轴时,S△OAM取得最大值$\frac{1}{2}$c=1,解得c=2,∴$a=\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{3}$.
(2)证明:当点M为椭圆的短轴的一个端点时,不妨设为(0,1),∵AB∥OM,则AB⊥x轴,|FA|=|FB|=$\frac{{b}^{2}}{a}$=$\frac{1}{a}$,∴|FA|•|FB|=$\frac{|OM{|}^{2}}{{a}^{2}}$=$\frac{1}{{a}^{2}}$.
当点M不为椭圆的短轴的一个端点时,设直线OM的方程为:y=kx,联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+{a}^{2}{y}^{2}={a}^{2}}\end{array}\right.$,解得x2=$\frac{{a}^{2}}{1+{k}^{2}{a}^{2}}$,y2=$\frac{{k}^{2}{a}^{2}}{1+{k}^{2}{a}^{2}}$,
∴|OM|2=x2+y2=$\frac{{a}^{2}(1+{k}^{2})}{1+{k}^{2}{a}^{2}}$.
直线AB的方程为:y=k(x+c),联立$\left\{\begin{array}{l}{y=k(x+c)}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$,化为:(1+a2k2)x2+2a2k2cx+a2c2k2-a2=0,
∴x1+x2=$\frac{-2{a}^{2}{k}^{2}c}{1+{a}^{2}{k}^{2}}$,x1x2=$\frac{{a}^{2}{c}^{2}{k}^{2}-{a}^{2}}{1+{a}^{2}{k}^{2}}$.
∴|FA|•|FB|=(ex1+a)(ex2+a)=e2x1x2+ae(x1+x2)+a2=$\frac{{c}^{2}}{{a}^{2}}$$•\frac{{a}^{2}({c}^{2}{k}^{2}-1)}{1+{a}^{2}{k}^{2}}$-$\frac{2{a}^{2}{k}^{2}{c}^{2}}{1+{a}^{2}{k}^{2}}$+a2=$\frac{{k}^{2}+1}{1+{a}^{2}{k}^{2}}$,(a2-c2=1).
∴|FA|•|FB|=$\frac{|OM{|}^{2}}{{a}^{2}}$.
综上可得:|FA|•|FB|=$\frac{|OM{|}^{2}}{{a}^{2}}$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交弦长问题、点到直线的距离公式、三角形面积计算公式、不等式的性质,考查了分类讨论推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
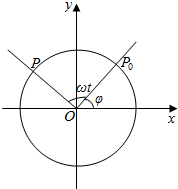 如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.
如图,点P是半径为rcm的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针以角速度ωrαd/s做圆周运动,求点P的纵坐标y关于时间t的函数关系,并求点P的运动周期和频率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com