已知数列{an}的各项均为正数,记A(n)=a1+a2+…+an,B(n)=a2+a3+…+an+1,C(n)=a3+a4+…+an+2,n=1,2,….
(1)若a1=1,a2=5,且对任意n∈N*,三个数A(n),B(n),C(n)组成等差数列,求数列{an}的通项公式.
(2)证明:数列{an}是公比为q的等比数列的充分必要条件是:对任意n∈N*,三个数A(n),B(n),C(n)组成公比为q的等比数列.
解:(1)∵对任意n∈N
*,三个数A(n),B(n),C(n)组成等差数列,
∴B(n)-A(n)=C(n)-B(n),
即a
n+1-a
1=a
n+2-a
2,亦即a
n+2-a
n+1=a
2-a
1=4.
故数列{a
n}是首项为1,公差为4的等差数列,于是a
n=1+(n-1)×4=4n-3.
(2)证明:(必要性):若数列{a
n}是公比为q的等比数列,对任意n∈N
*,有a
n+1=a
nq.由a
n>0知,A(n),B(n),C(n)均大于0,于是
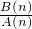
=

=
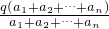
=q,
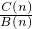
=
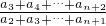
=
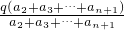
=q,
即
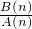
=
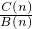
=q,
∴三个数A(n),B(n),C(n)组成公比为q的等比数列;
(充分性):若对任意n∈N
*,三个数A(n),B(n),C(n)组成公比为q的等比数列,则
B(n)=qA(n),C(n)=qB(n),
于是C(n)-B(n)=q[B(n)-A(n)],即a
n+2-a
2=q(a
n+1-a
1),亦即a
n+2-qa
n+1=a
2-qa
1.
由n=1时,B(1)=qA(1),即a
2=qa
1,从而a
n+2-qa
n+1=0.
∵a
n>0,
∴
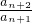
=

=q.故数列{a
n}是首项为a
1,公比为q的等比数列.
综上所述,数列{a
n}是公比为q的等比数列的充分必要条件是:对任意n∈N
*,三个数A(n),B(n),C(n)组成公比为q的等比数列.
分析:(1)由于对任意n∈N
*,三个数A(n),B(n),C(n)组成等差数列,可得到B(n)-A(n)=C(n)-B(n),即a
n+1-a
1=a
n+2-a
2,整理即可得数列{a
n}是首项为1,公差为4的等差数列,从而可得a
n.
(2)必要性:由数列{a
n}是公比为q的等比数列,可证得即
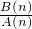
=
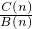
=q,即必要性成立;
充分性:若对任意n∈N
*,三个数A(n),B(n),C(n)组成公比为q的等比数列,可得a
n+2-qa
n+1=a
2-qa
1.由n=1时,B(1)=qA(1),即a
2=qa
1,从而a
n+2-qa
n+1=0,即充分性成立,于是结论得证.
点评:本题考查等差数列的性质,考查充要条件的证明,考查等比关系的确定,突出化归思想,逻辑思维与综合运算能力的考查,属于难题.

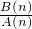 =
= =
=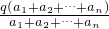 =q,
=q,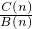 =
=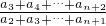 =
=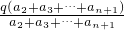 =q,
=q,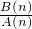 =
=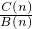 =q,
=q,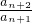 =
= =q.故数列{an}是首项为a1,公比为q的等比数列.
=q.故数列{an}是首项为a1,公比为q的等比数列.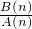 =
=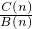 =q,即必要性成立;
=q,即必要性成立;

 阅读快车系列答案
阅读快车系列答案 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)