
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 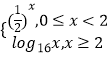 ,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
【答案】![]()
【解析】解:由题意,f(x)在(﹣∞,﹣2]和[0,2)上是减函数,在(﹣2,0]和[2,+∞)上是增函数;
∴x=0时,函数取极大值1,x=±2时,取极小值 ![]() ,且|x|≥16时,f(x)≥1,则f(x)的图象如下所示:
,且|x|≥16时,f(x)≥1,则f(x)的图象如下所示: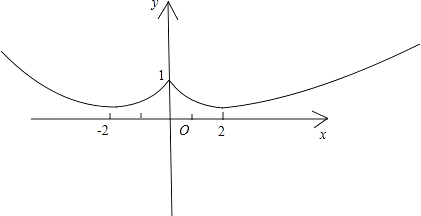
由[f(x)]2+af(x)﹣a﹣1=0得[f(x)﹣1][f(x)+a+1]=0;
∴f(x)=1或﹣a﹣1;
∵关于x的方程[f(x)]2+af(x)﹣a﹣1=0有7个不同实数根;
∴ ![]() ;
;
∴ ![]() ;
;
∴a的取值范围为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】某地区2008年至2016年粮食产量的部分数据如下表:

(1)求该地区2008年至2016年的粮食年产量![]() 与年份
与年份![]() 之间的线性回归方程;
之间的线性回归方程;
(2)利用(1)中的回归方程,分析2008年至2016年该地区粮食产量的变化情况,并预测该地区 2018年的粮食产量.
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明.
(1)用数学归纳法证明:12+22+32+…+n2= ![]() ,n是正整数;
,n是正整数;
(2)用数学归纳法证明不等式:1+ ![]() +
+ ![]() +…+
+…+ ![]() <2
<2 ![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0013,那么抽取的第40个号码 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com