
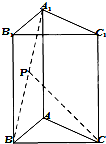
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.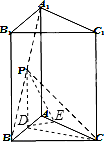
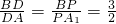 ,∴
,∴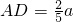 .
.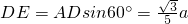 ,
,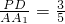 ,∴
,∴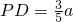 ,∴
,∴ ,∴P-AC-B的大小为∠PED=60°.…12
,∴P-AC-B的大小为∠PED=60°.…12 设P(x,0,z),则B(a,0,0)、A1(0,0,a)、
设P(x,0,z),则B(a,0,0)、A1(0,0,a)、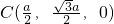 .
.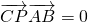 得
得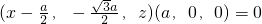 ,即
,即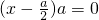 ,
,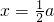 ,即P为A1B的中点,也即A1P:PB=1时,PC⊥AB.…4′
,即P为A1B的中点,也即A1P:PB=1时,PC⊥AB.…4′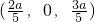 .
. .则
.则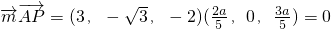 ,
,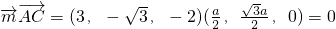 .
. 是平面PAC的一个法向量.
是平面PAC的一个法向量.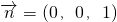 .
.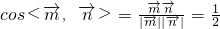 ,∴二面角P-AC-B的大小是60°.…(12分)
,∴二面角P-AC-B的大小是60°.…(12分)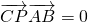 ,可确定A1P:PB的值,使得PC⊥AB;
,可确定A1P:PB的值,使得PC⊥AB;

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.| A1P |
| PB |
| A1P |
| PB |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
| ||
| 48 |
| ||
| 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com