
【题目】设曲线![]() 上一点
上一点![]() 到焦点的距离为3.
到焦点的距离为3.
(1)求曲线C方程;
(2)设P,Q为曲线C上不同于原点O的任意两点,且满足以线段PQ为直径的圆过原点O,试问直线PQ是否恒过定点?若恒过定点,求出定点坐标;若不恒过定点,说明理由.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
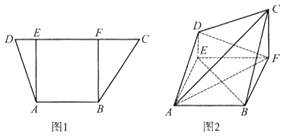
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC(如图一)的平面展开图(如图二)中,四边形ABCD为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥P-ABC中:
均为正三角形,在三棱锥P-ABC中:
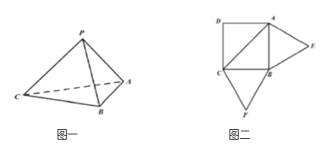
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上运动,当直线BM与平面PAC所成的角最大时,求直线MA与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到![]() 列联表如下:
列联表如下:
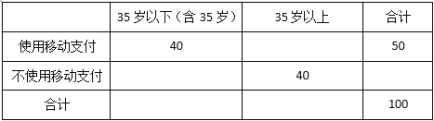
(1)将上![]() 列联表补充完整,并请说明在犯错误的概率不超过0.10的前提下,认为支付方式与年龄是否有关?
列联表补充完整,并请说明在犯错误的概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.

(参考公式: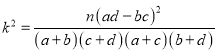 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为![]() 、
、![]() 、
、![]() ,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
,笔试、口试、实验通过考试分别记4分、2分、4分,没通过的项目记0分,各项成绩互不影响.
(Ⅰ)若规定总分不低于8分即可进入复赛,求甲同学进入复赛的概率;
(Ⅱ)记三个项目中通过考试的个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
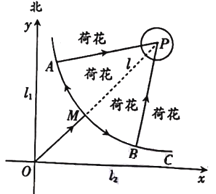
【题目】如图,某市建有贯穿东西和南北的两条垂直公路![]() ,
,![]() ,在它们交叉路口点
,在它们交叉路口点![]() 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台![]() 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线![]() 上,
上,![]() 与环形公路的交点记作
与环形公路的交点记作![]() .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路![]() 先到达环形公路
先到达环形公路![]() 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路![]() ,
,![]() 的环形公路上选
的环形公路上选![]() ,
,![]() 两处(
两处(![]() ,
,![]() 关于直线
关于直线![]() 对称)修建直达观景台
对称)修建直达观景台![]() 的玻璃栈道
的玻璃栈道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的环形公路可用曲线
的环形公路可用曲线![]() 近似表示,曲线
近似表示,曲线![]() 符合函数
符合函数![]() .
.
(1)若![]() 百米,点
百米,点![]() 到
到![]() 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道![]() 的总长度;
的总长度;
(2)若要使得玻璃栈道![]() 的总长度最小为
的总长度最小为![]() 百米,求观景台
百米,求观景台![]() 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com