
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知首项大于0的等差数列![]() 的公差
的公差![]() ,且
,且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;
;
①求数列![]() 的通项
的通项![]() ;
;
②是否存在实数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若
,若![]() (
(![]() 是与
是与![]() 无关的常数,
无关的常数,![]() )则称数列
)则称数列![]() 叫做“弱等差数列”已知数列
叫做“弱等差数列”已知数列![]() 满足:
满足:![]() 且
且![]() ,对于
,对于![]() 恒成立,(其中
恒成立,(其中![]() 都是常数)
都是常数)
(1)求证:数列![]() 是“弱等差数列”,并求出数列
是“弱等差数列”,并求出数列![]() 的通项公式
的通项公式
(2)当![]() 时,若数列
时,若数列![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围
的取值范围
(3)若![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 、
、![]() 与平面
与平面![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
B.![]() 是
是![]() 的充要条件
的充要条件
C.设![]() ,则
,则![]() 是
是![]() 的必要不充分条件
的必要不充分条件
D.设![]() ,则
,则![]() 是
是![]() 的既不充分也不必要条件
的既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司举办捐步公益活动,参与者通过捐赠每天的运动步数获得公司提供的牛奶,再将牛奶捐赠给留守儿童.此活动不但为公益事业作出了较大的贡献,公司还获得了相应的广告效益.据测算,首日参与活动人数为![]() 人,以后每天人数比前一天都增加
人,以后每天人数比前一天都增加![]() ,
,![]() 天后捐步人数稳定在第
天后捐步人数稳定在第![]() 天的水平,假设此项活动的启动资金为
天的水平,假设此项活动的启动资金为![]() 万元,每位捐步者每天可以使公司收益
万元,每位捐步者每天可以使公司收益![]() 元(以下人数精确到
元(以下人数精确到![]() 人,收益精确到
人,收益精确到![]() 元).
元).
(1)求活动开始后第![]() 天的捐步人数,及前
天的捐步人数,及前![]() 天公司的捐步总收益;
天公司的捐步总收益;
(2)活动开始第几天以后公司的捐步总收益可以收回启动资金并有盈余?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区的“微信健步走”活动情况,现用分层抽样的方法从中抽取老、中、青三个年龄段人员进行问卷调查.已知抽取的样本同时满足以下三个条件:
(i)老年人的人数多于中年人的人数;
(ii)中年人的人数多于青年人的人数;
(iii)青年人的人数的两倍多于老年人的人数.
①若青年人的人数为4,则中年人的人数的最大值为___________.
②抽取的总人数的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
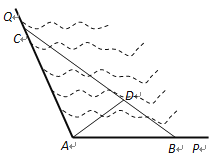
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com