
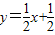 与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;
与抛物线交于点E.问:在抛物线的对称轴上是否存在这样的点F,使得△ABE与以B、D、F为顶点的三角形相似,若存在,求出点F的坐标;若不存在,请说明理由;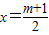 ,由A(-x,0),知
,由A(-x,0),知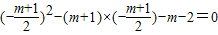 ,由此能求出这个二次函数的解析式.
,由此能求出这个二次函数的解析式.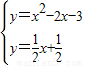 ,得到点E的坐标为(
,得到点E的坐标为(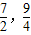 ).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE=
).过点E作EH⊥x轴于H.在Rt△AEH中,可求AE=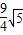 ,若对称轴与直线
,若对称轴与直线 交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要
交于点P,P点坐标为(1,1).由∠PAM=∠MDB,知要使得在抛物线的对称轴上存在点F,使得△ABE与以B、D、F为顶点的三角形相似,只需要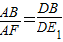 或
或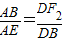 .由此能求出符合题意的F点坐标.
.由此能求出符合题意的F点坐标.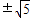 ,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG=
,1),由A、B、G在同一圆上,知圆心一定在抛物线的对称轴上,由PA=PA=PG=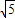 ,知点P即为过点A、B、G的圆的圆心.
,知点P即为过点A、B、G的圆的圆心.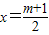 ,
, ,
, (舍).
(舍).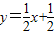 与抛物线交于点E,
与抛物线交于点E,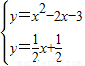 ,
,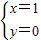 或
或 ,
, ).
).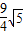 .
. 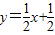 交于点P,
交于点P,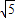 ,
,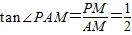 ,
,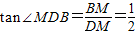 ,
,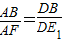 或
或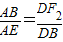 .
.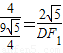 ,
,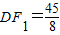 ,
,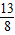 ).
).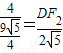 ,
,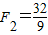 ,
, ).
).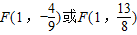 .
.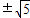 ,1),
,1), ,
,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| d2 |
| d1 |
| ||
| 2 |
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| d2 |
| d1 |
| ||
| 2 |
| S | 2 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 9 |
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
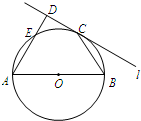 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
|
|
| π |
| 2 |
| π |
| 4 |
| a2+b2 |
| c2+d2 |
| (ac+bd)(ad+bc) |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com