
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 相切或相交 |
分析 由圆的方程找出圆心坐标与半径,因为M为圆内一点,所以M到圆心的距离小于圆的半径,利用两点间的距离公式表示出一个不等式,然后利用点到直线的距离公式表示出圆心到已知直线的距离d,根据求出的不等式即可得到d大于半径r,得到直线与圆的位置关系是相离.
解答 解:由圆的方程得到圆心坐标为(0,0),半径r=a,
由M为圆内一点得到:$\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}$<a,
则圆心到已知直线的距离d=$\frac{|-{a}^{2}|}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$>a=r,
所以直线与圆的位置关系为:相离.
故选C.
点评 此题考查小时掌握点与圆的位置关系及直线与圆的位置关系的判断方法,灵活运用两点间的距离公式及点到直线的距离公式化简求值,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$) | B. | (-$\frac{e}{2}$,0] | C. | ($\frac{9}{2}$e${\;}^{-\frac{3}{2}}$,+∞) | D. | (-$\frac{e}{2}$,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
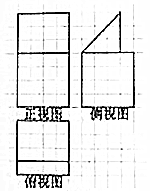
| A. | 93+12$\sqrt{2}$ | B. | 97+12$\sqrt{2}$ | C. | 105+12$\sqrt{2}$ | D. | 109+12$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com