
对于函数y=f(x)(x∈D,D是此函数的定义域)若同时满足下列条件:
(Ⅰ)f(x)在D内单调递增或单调递减;
(Ⅱ)存在区间[a,b]![]() D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=![]() 符合条件(Ⅱ)的区间[a,b];
符合条件(Ⅱ)的区间[a,b];
(2)判断函数f(x)=![]() (x∈
(x∈![]() )是否为闭函数?并说明理由;
)是否为闭函数?并说明理由;
(3)若y=![]() 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)f(x)在D内单调递增或单调递减;
(Ⅱ)存在区间[a,b]![]() D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=![]() 符合条件(Ⅱ)的区间[a,b];
符合条件(Ⅱ)的区间[a,b];
(2)判断函数f(x)=![]() (x∈
(x∈![]() )是否为闭函数?并说明理由;
)是否为闭函数?并说明理由;
(3)若y=![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西赣州会昌中学高二下学期第一次月考理科数学试卷(带解析) 题型:填空题
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点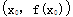 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
若函数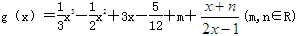 ,
,
则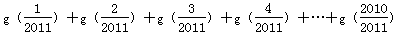 = .
= .
查看答案和解析>>
科目:高中数学 来源:2014届江西赣州会昌中学高二下学期第一次月考理科数学试卷(解析版) 题型:填空题
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
若函数 ,
,
则 = .
= .
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修1函数的概念练习卷(解析版) 题型:选择题
对于函数y=f(x),以下说法正确的有…( )
①y是x的函数
②对于不同的x,y的值也不同
③f(a)表示当x=a时函数f(x)的值,是一个常量
④f(x)一定可以用一个具体的式子表示出来
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com